题目描述:翻转一棵二叉树。
示例:
输入:
1 | 4 |
输出:
1 | 4 |
1 | /** |
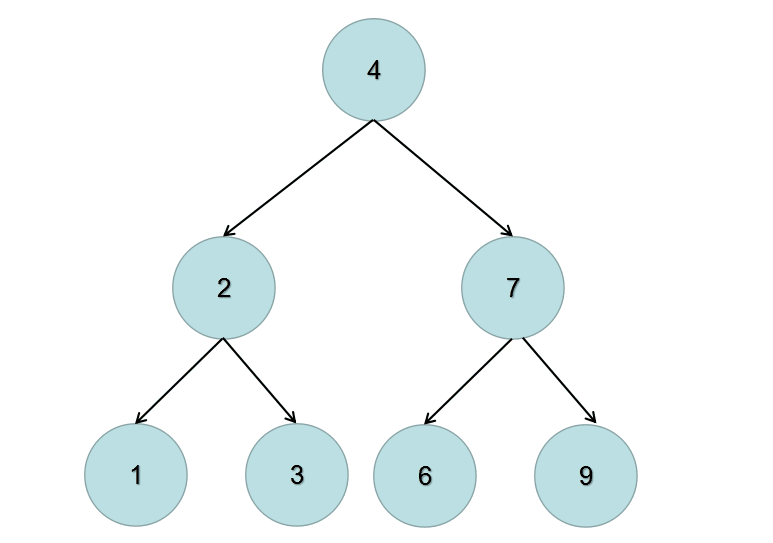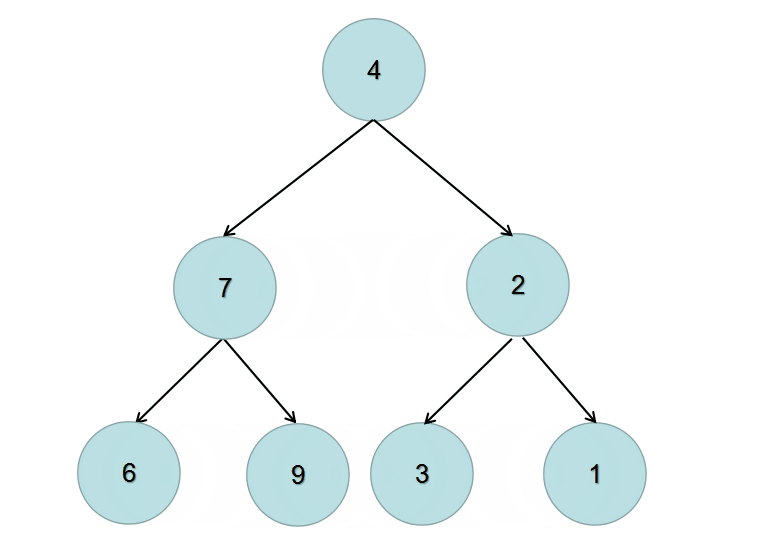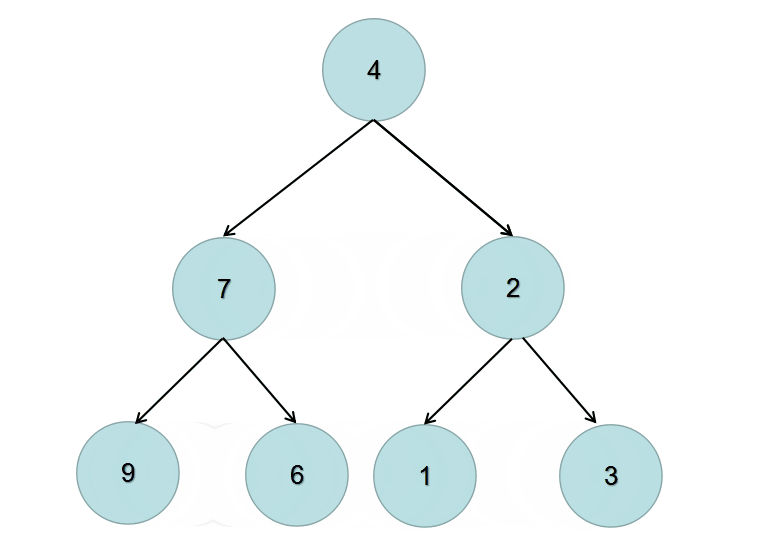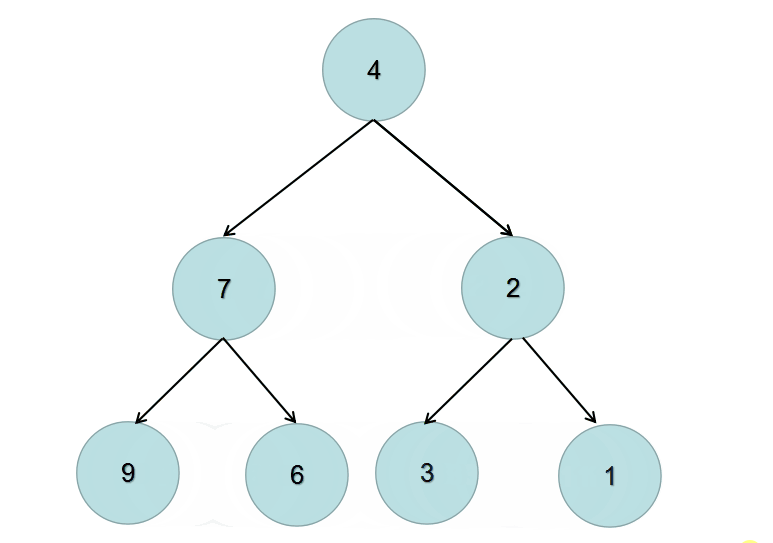
方法一:递归 / 深度优先搜索dfs
递归的两个条件如下:
- 终止条件:当前节点为 null 时返回
- 交换当前节点的左右节点,再递归的交换当前节点的左节点,递归的交换当前节点的右节点
1 | class Solution { |
复杂度分析:
- 时间复杂度:每个元素都必须访问一次,所以是 O(n)
- 空间复杂度:最坏的情况下(当二叉树退化为链表),需要存放 O(n) 个函数调用
执行结果:通过
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:37.2 MB, 在所有 Java 提交中击败了76.28%的用户
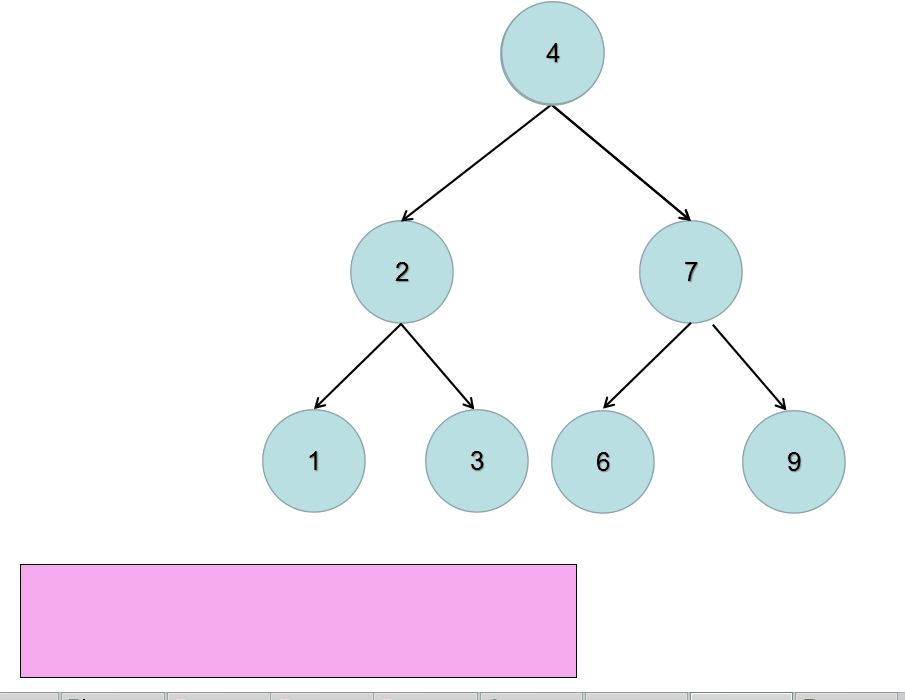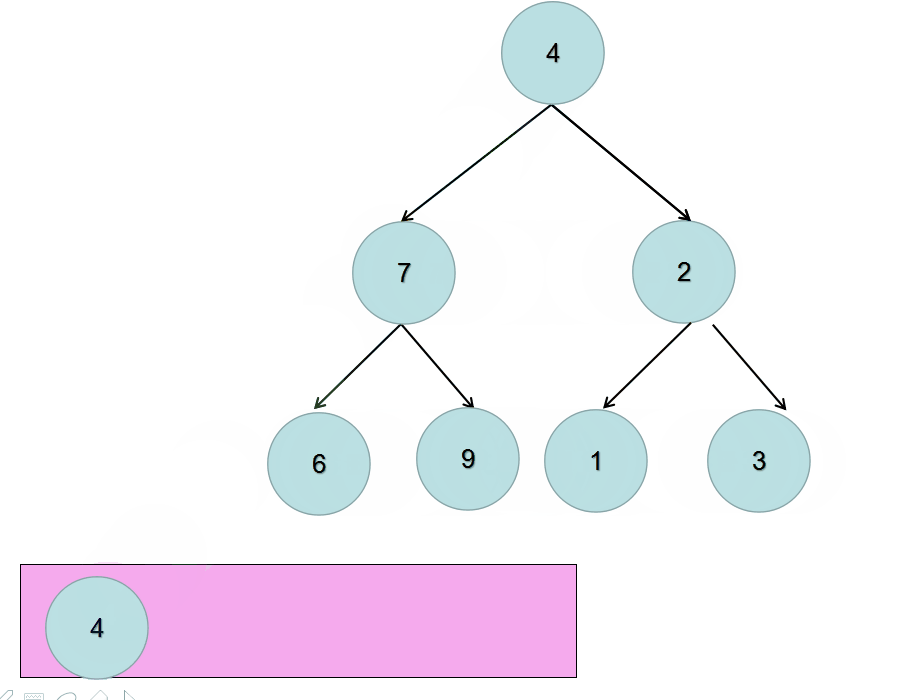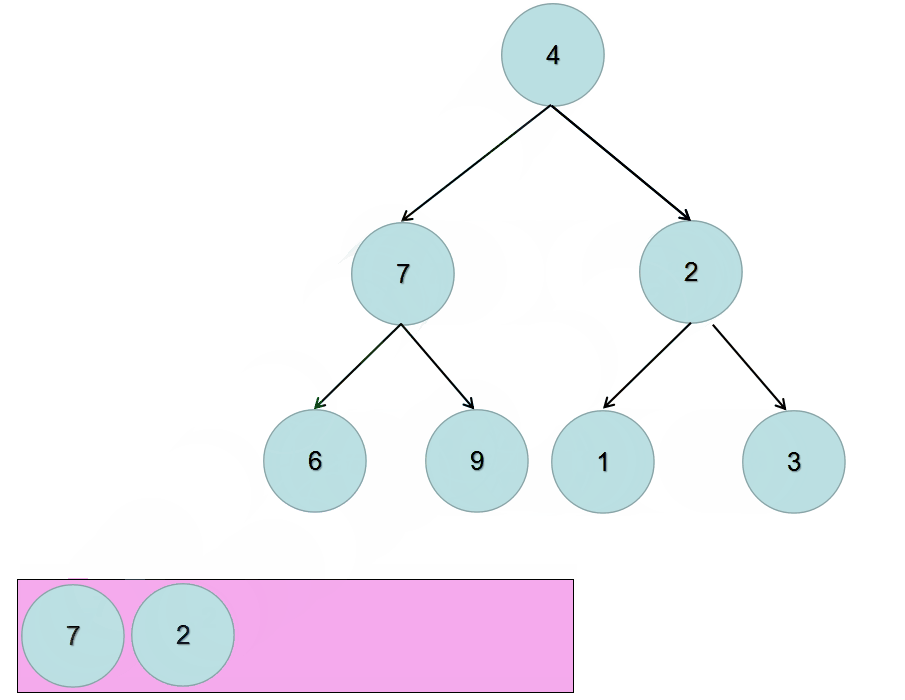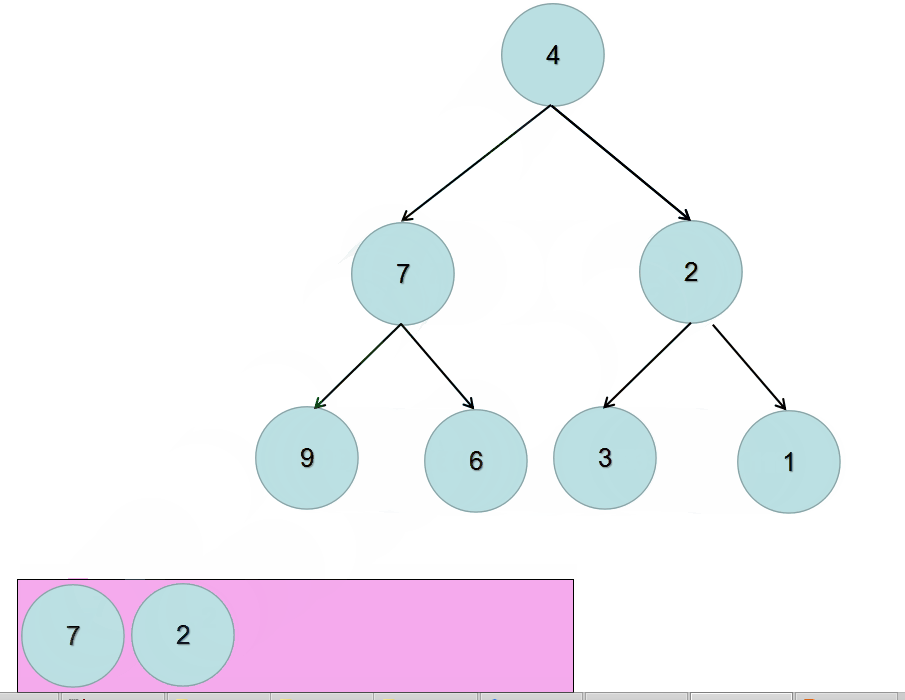
方法二:迭代 / 广度优先搜索bfs
广度优先遍历需要额外的数据结构–队列,来存放临时遍历到的元素。
深度优先遍历的特点是一竿子插到底,不行了再退回来继续;而广度优先遍历的特点是层层扫荡。
所以,我们需要先将根节点放入到队列中,然后不断的迭代队列中的元素。对当前元素调换其左右子树的位置,然后:
- 判断其左子树是否为空,不为空就放入队列中
- 判断其右子树是否为空,不为空就放入队列中
1 | class Solution { |
复杂度分析:
- 时间复杂度:同样每个节点都需要入队列/出队列一次,所以是 O(n)
- 空间复杂度:最坏的情况下会包含所有的叶子节点,完全二叉树叶子节点是 n/2 个,所以时间复杂度是 O(n)
执行结果:通过
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:37.3 MB, 在所有 Java 提交中击败了47.08%的用户