对称二叉树

发表于 | 分类于 |
字数统计: 1.3k 字 | 阅读时长 ≈ 5 分钟

题目描述：给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1
2
3
4
5
     1
   /   \
  2     2
 / \   / \
3   4 4   3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1
2
3
4
5
 1
/  \
2   2
 \   \
 3    3

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
  public boolean isSymmetric(TreeNode root) {

  }
}

方法一：递归

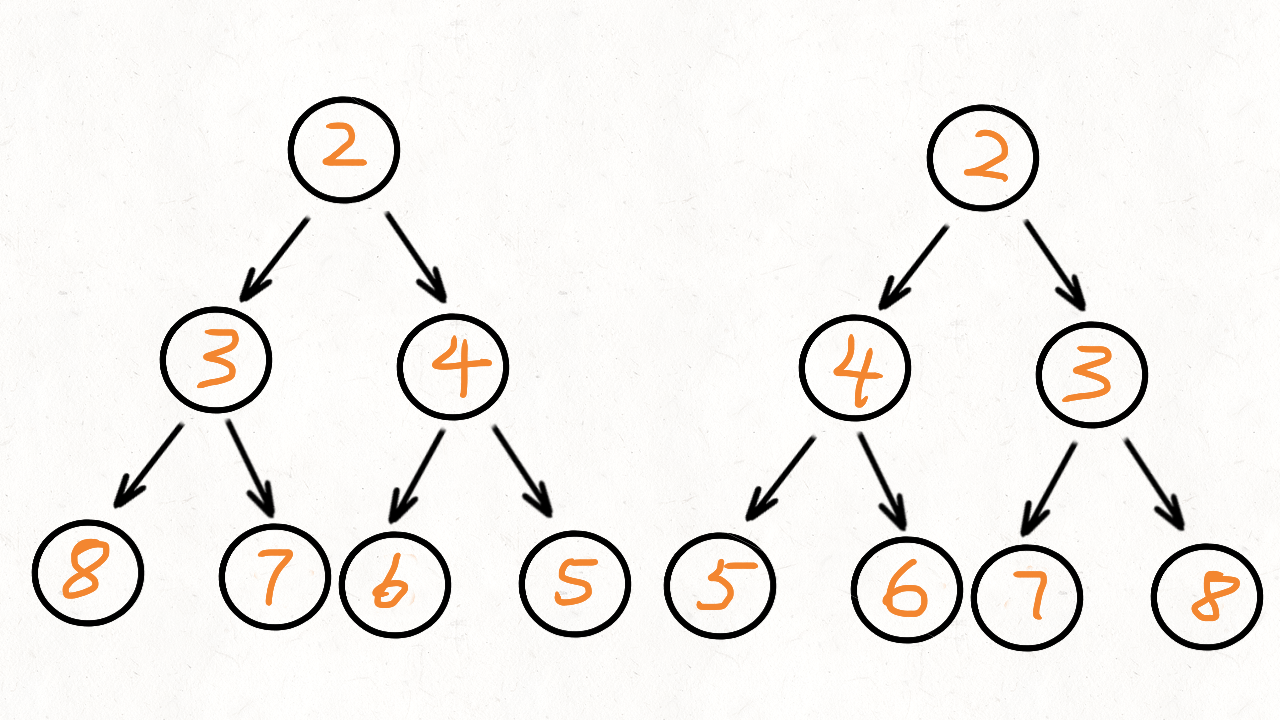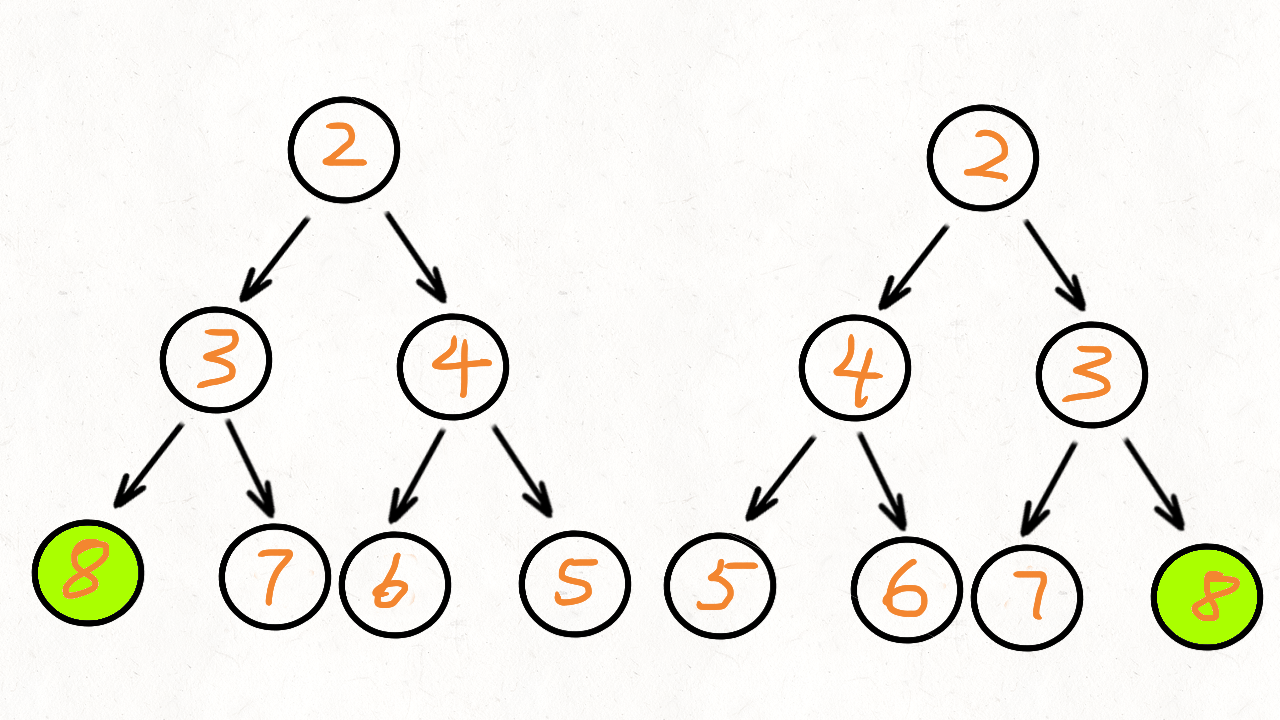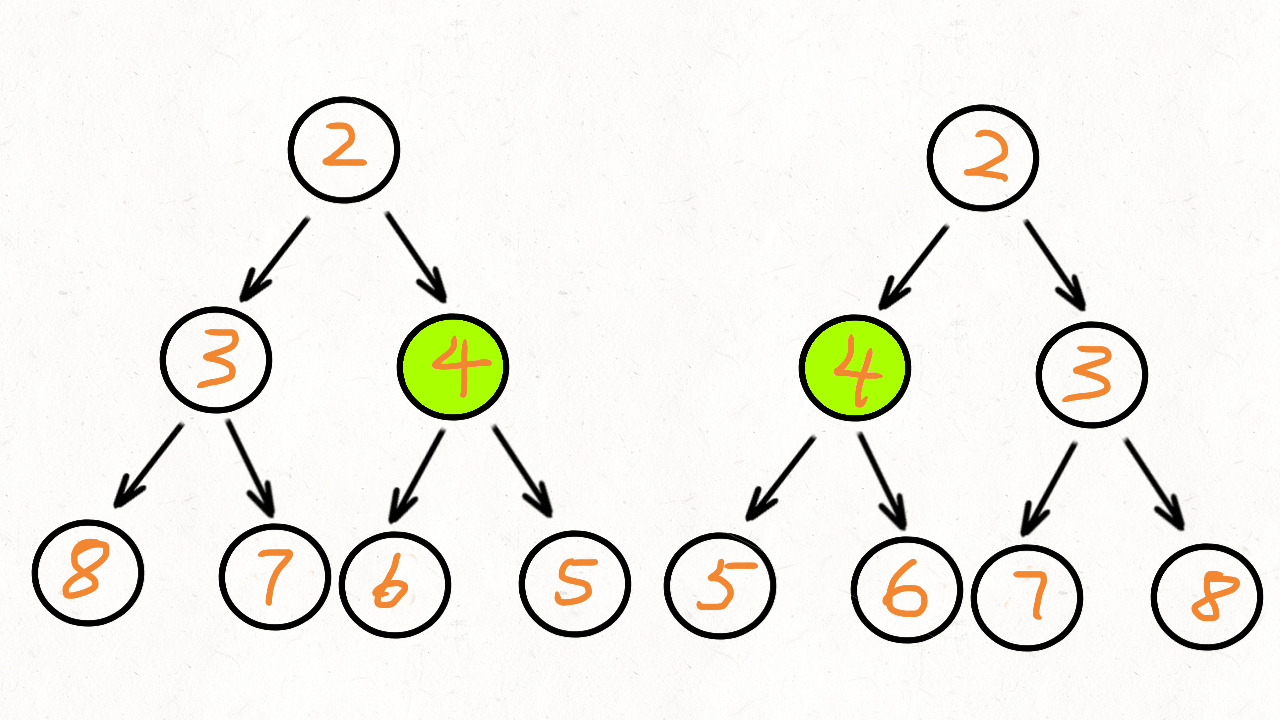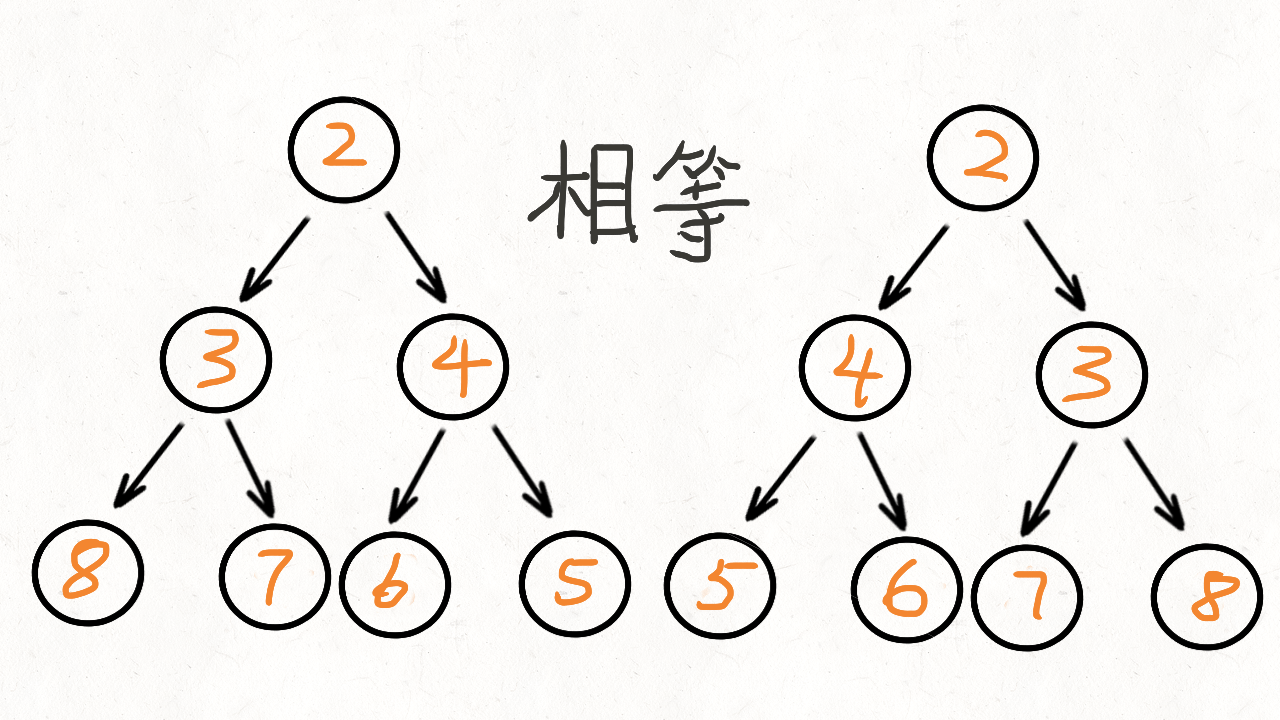
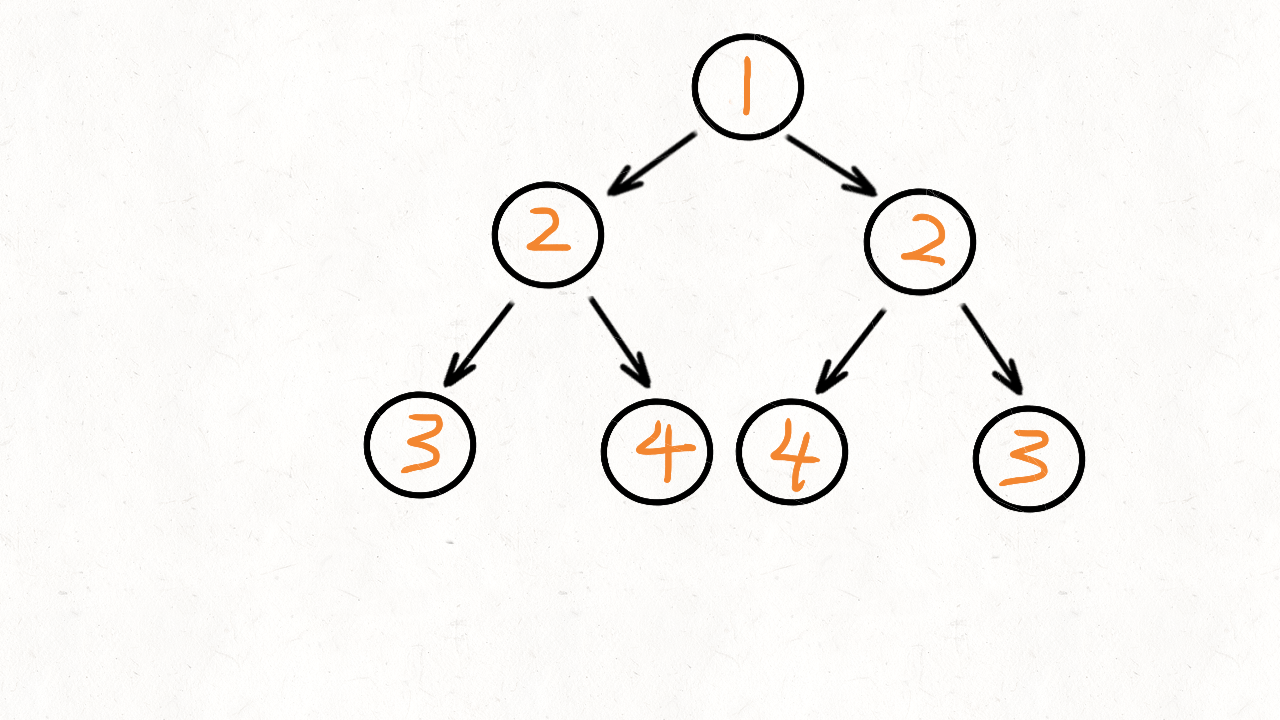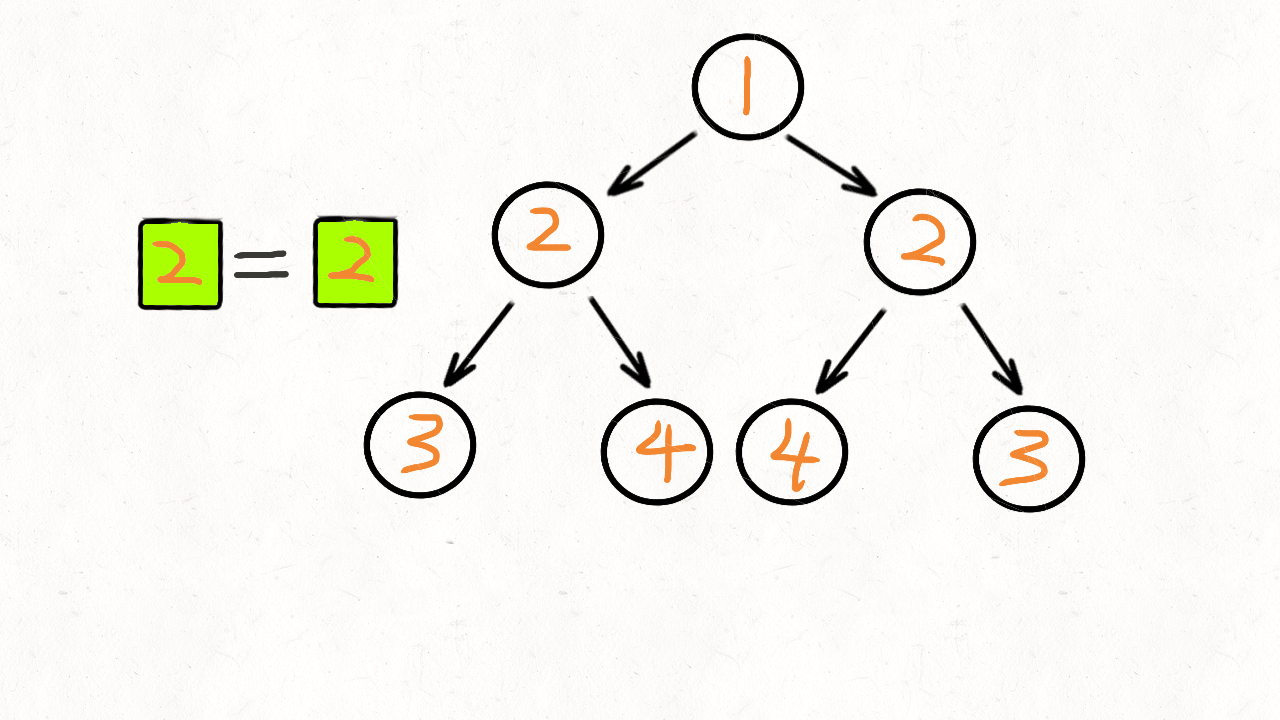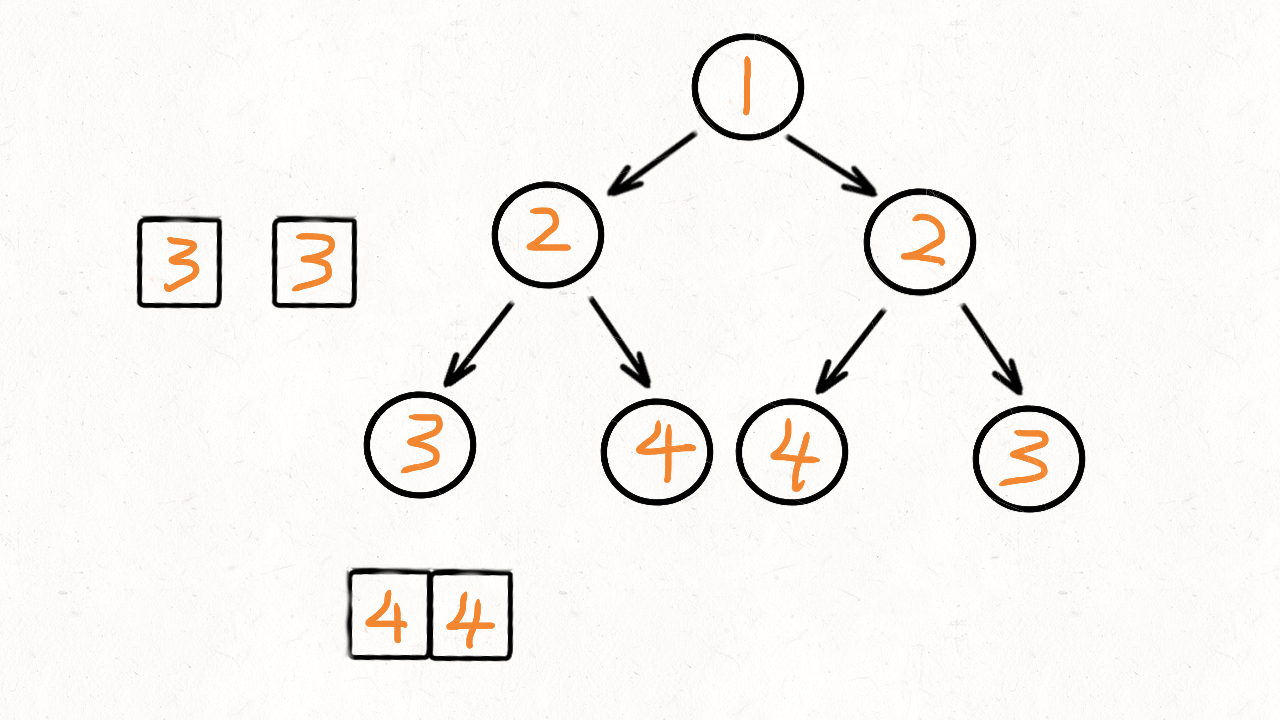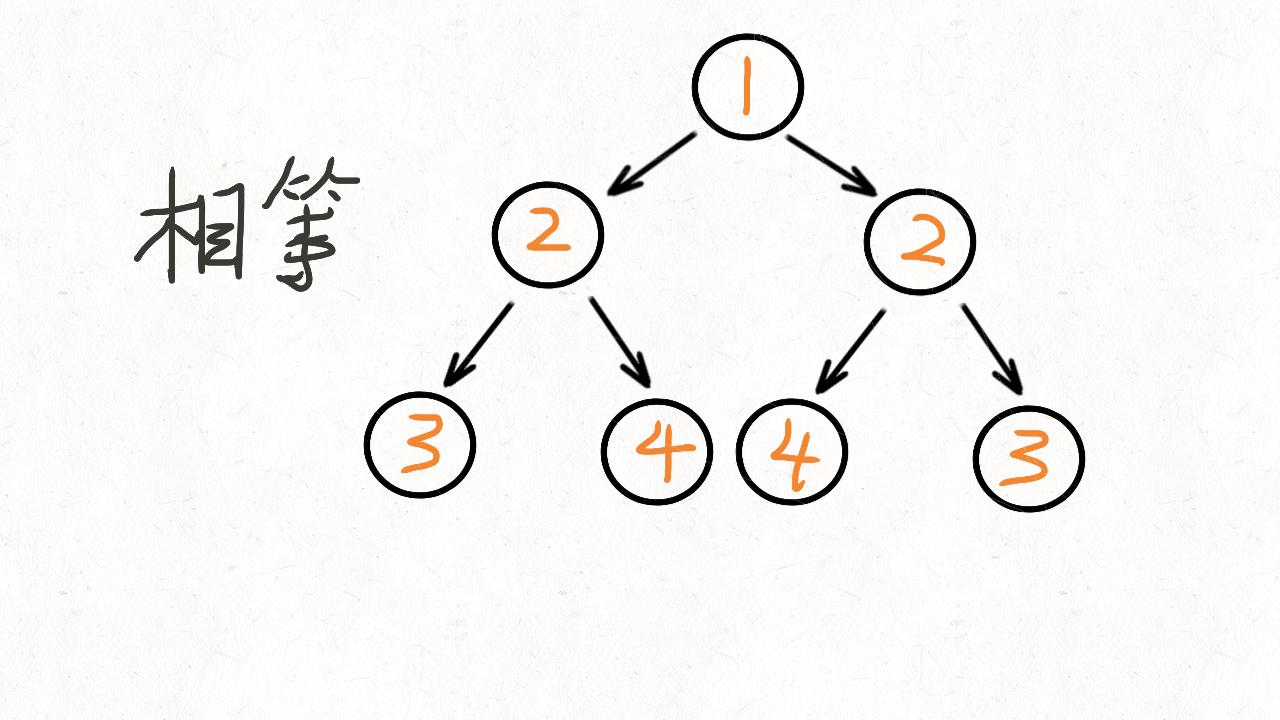
根据题目的描述，镜像对称，就是左右两边相等，也就是左子树和右子树是相当的。我们将根节点的左子树记做 p，右子树记做 q。比较 p 是否等于 q，不等的话直接返回就可以了。如果相当，比较 p 的左节点和 q 的右节点，再比较 p 的右节点和 q 的左节点

根据上面信息可以总结出递归函数的两个终止条件：

  • p 和 q 不等、 p 和 q 都为空、p 和 q 有一个为空
  • 递归比较 p 的 left 和 right，递归比较 q 的 left 和 right
2.gif 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
  public boolean isSymmetric(TreeNode root) {
    if(root == null) return true;
    // 调用递归函数，比较左节点，右节点
    return dfs(root.left, root.right);
  }

  private boolean dfs(TreeNode p, TreeNode q) {
    // 递归的终止条件是两个节点都为空
    // 或者两个节点中有一个为空
    // 或者两个节点的值不相等
    if(p == null && q == null) return true;
    if(p == null || q == null) return false;
    if(p.val != q.val) return false;
    // 再递归的比较 左节点的左孩子 和 右节点的右孩子
    // 以及比较 左节点的右孩子 和 右节点的左孩子
    return dfs(p.left, q.right) && dfs(p.right, q.left);
  }
}

var isSymmetric = function(root) {
  if(!root) return true
  // 调用递归函数，比较左节点，右节点
  return isSame(root.left, root.right)
};

var isSame = function(p, q) {
  // 递归的终止条件是两个节点都为空
  // 或者两个节点中有一个为空
  // 或者两个节点的值不相等
  if(!p && !q) return true
  if(!p || !q) return false
  if(p.val !== q.val) return false
  // 再递归的比较 左节点的左孩子 和 右节点的右孩子
  // 以及比较 左节点的右孩子 和 右节点的左孩子
  return isSame(p.left, q.right) && isSame(p.right, q.left)
}

复杂度分析：

  • 时间复杂度：这里遍历了这棵树，渐进时间复杂度为 O(n)
  • 空间复杂度：这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 h，故渐进空间复杂度为 O(h)

执行结果：通过

  • 执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户

  • 内存消耗：38.1 MB, 在所有 Java 提交中击败了41.89%的用户

方法二：遍历

递归程序改写成迭代程序的常用方法：引入队列

思路如下：

  • 首先从队列中拿出两个节点(p 和 q)比较
  • 将 p 的 left 节点和 q 的 right 节点放入队列
  • 将 p 的 right 节点和 q 的 left 节点放入队列
1.gif 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
  public boolean isSymmetric(TreeNode root) {
    if(root == null || (root.left == null && root.right == null)) return true;
    // 用队列保存节点
    Queue<TreeNode> queue = new LinkedList<>();
    // 将根节点的左右孩子放到队列中
    queue.offer(root.left);
    queue.offer(root.right);
    while(!queue.isEmpty()) {
      // 从队列中取出两个节点，再比较这两个节点
      TreeNode p = queue.poll();
      TreeNode q = queue.poll();
      // 如果两个节点都为空就继续循环，两者有一个为空就返回false
      if(p == null && q == null) {
        continue;
      }
      if(p == null || q == null) {
        return false;
      }
      if(p.val != q.val) {
        return false;
      }
      // 将左节点的左孩子， 右节点的右孩子放入队列
      queue.offer(p.left);
      queue.offer(q.right);
      // 将左节点的右孩子，右节点的左孩子放入队列
      queue.offer(p.right);
      queue.offer(q.left);
    }
    return true;
  }
}

var isSymmetric = function(root) {
  if(!root) return true
  // 用队列保存节点
  let queue = []
  // 将根节点的左右孩子放到队列中
  queue.push(root.left)
  queue.push(root.right)
  while(queue.length) {
    // 从队列中取出两个节点，再比较这两个节点
    let p = queue.shift()
    let q = queue.shift()
    // 如果两个节点都为空就继续循环，两者有一个为空就返回false
    if(!p && !q) continue
    if(!p || !q) return false
    if(p.val !== q.val) return false
    // 将左节点的左孩子， 右节点的右孩子放入队列
    queue.push(p.left)
    queue.push(q.right)
    // 将左节点的右孩子，右节点的左孩子放入队列
    queue.push(p.right)
    queue.push(q.left)
  }
  return true
};

复杂度分析：

  • 时间复杂度：O(n)，同「方法一」
  • 空间复杂度：这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过 n 个点，故渐进空间复杂度为 O(n)

执行结果：通过

  • 执行用时：1 ms, 在所有 Java 提交中击败了29.33%的用户

  • 内存消耗：39.3 MB, 在所有 Java 提交中击败了12.87%的用户