杨辉三角

发表于 | 分类于 |
字数统计: 477 字 | 阅读时长 ≈ 2 分钟

题目描述：给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

在杨辉三角中，每个数是它左上方和右上方的数的和。

img

示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]

方法一：数学

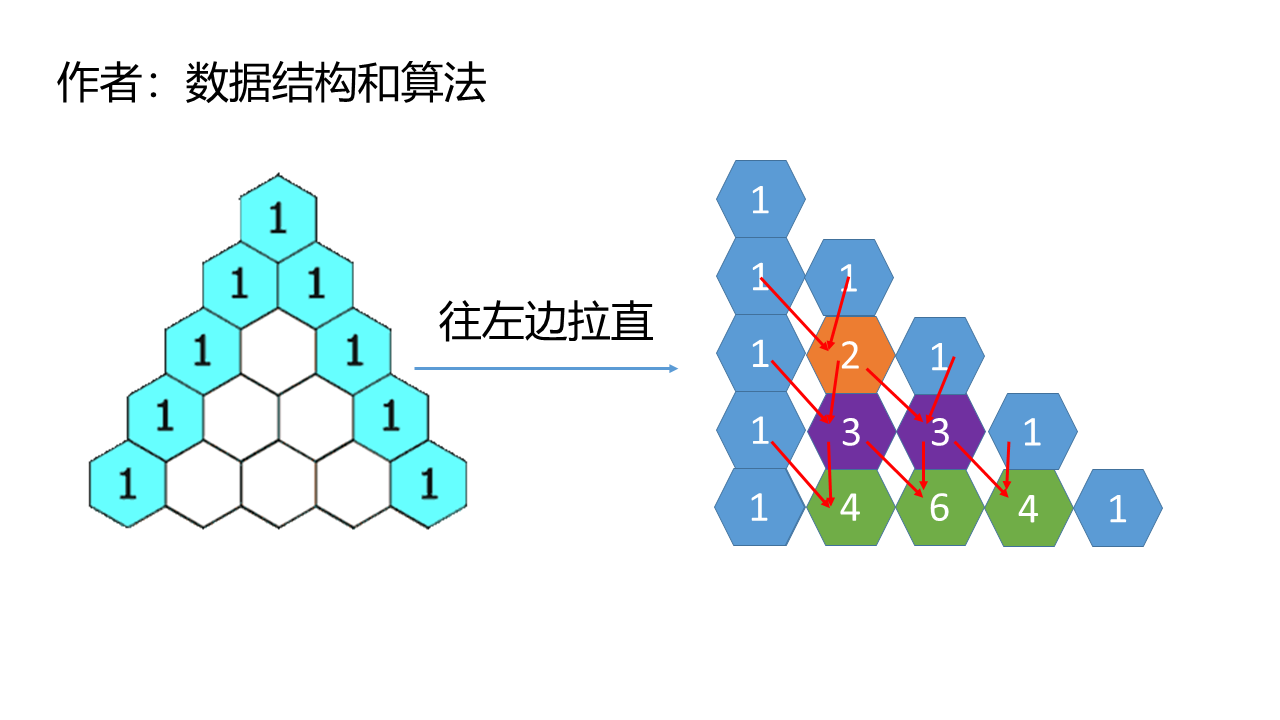
首先观察这个三角形的特点，杨辉三角形是一个等边三角形，其中左边和右边每个格子的值都是1。

三角形斜的不好看，如果我们把这个三角形往左边拉直就会发现，除了两边的都是1以外，其他每个格子的值都是他正上面格子和左上角格子的和。

leet0118.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
  public List<List<Integer>> generate(int numRows) {
    // 结果值
    List<List<Integer>> list = new ArrayList<>();
    // 每一行的元素
    ArrayList<Integer> row = new ArrayList<>();
    for(int i = 0; i < numRows; i++) {
      // 下面一行都会比上面一行多一个元素，我们在第一个位置给他加个1
      row.add(0, 1);
      // 遍历每一行的结果，遍历的时候跳过第一个和最后一个，
      // 每个格子的值都是他正上面和左上角元素的和
      for(int j = 1; j < row.size() - 1; j++) {
        row.set(j, row.get(j) + row.get(j + 1));
      }
      // 把结果存放到res中
      list.add(new ArrayList(row));
    }
    return list;
  }
}

var generate = function(numRows) {
  const ret = [];
  for (let i = 0; i < numRows; i++) {
    const row = new Array(i + 1).fill(1);
    for (let j = 1; j < row.length - 1; j++) {
      row[j] = ret[i - 1][j - 1] + ret[i - 1][j];
    }
    ret.push(row);
  }
  return ret;
};

复杂度分析

  • 时间复杂度：O(numRows2)。
  • 空间复杂度：O(1)。不考虑返回值的空间占用。

执行结果：通过

  • 执行用时：1 ms, 在所有 Java 提交中击败了54.68%的用户

  • 内存消耗：36.5 MB, 在所有 Java 提交中击败了21.42%的用户