数组中的第K个最大元素

发表于 | 分类于 |
字数统计: 3k 字 | 阅读时长 ≈ 13 分钟

题目描述：在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明:
你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

方法一：暴力

1
2
3
4
5
6
7
8
9
10
11
class Solution {
  public int findKthLargest(int[] nums, int k) {
    Arrays.sort(nums);
    return nums[nums.length - k];
  }
}

var findKthLargest = function(nums, k) {
  nums.sort((a, b) => a - b)
  return nums[nums.length - k]
};

复杂度分析：

  • 时间复杂度：O(NlogN)，这里 N 是数组的长度，算法的性能消耗主要在排序，JDK 默认使用快速排序，因此时间复杂度为 O(NlogN)。
  • 空间复杂度：O(1)，这里是原地排序，没有借助额外的辅助空间。

执行结果：通过

  • 执行用时：2 ms, 在所有 Java 提交中击败了91.30%的用户
  • 内存消耗：38.5 MB, 在所有 Java 提交中击败了87.53%的用户

方法二：基于快速排序的选择方法

思想

  • 通过 paritition 减治
  • partition（切分）操作总能排定一个元素，还能够知道这个元素它最终所在的位置，这样每经过一次 partition（切分）操作就能缩小搜索的范围
  • 切分过程可以不借助额外的数组空间，仅通过交换数组元素实现

paritition 切分操作

  • 对于某个索引 j，nums[j] 已经排定，即 nums[j] 经过 partition（切分）操作以后会放置在它 “最终应该放置的地方”；
  • nums[left] 到 nums[j - 1] 中的所有元素都不大于 nums[j]；
  • nums[j + 1] 到 nums[right] 中的所有元素都不小于 nums[j]。
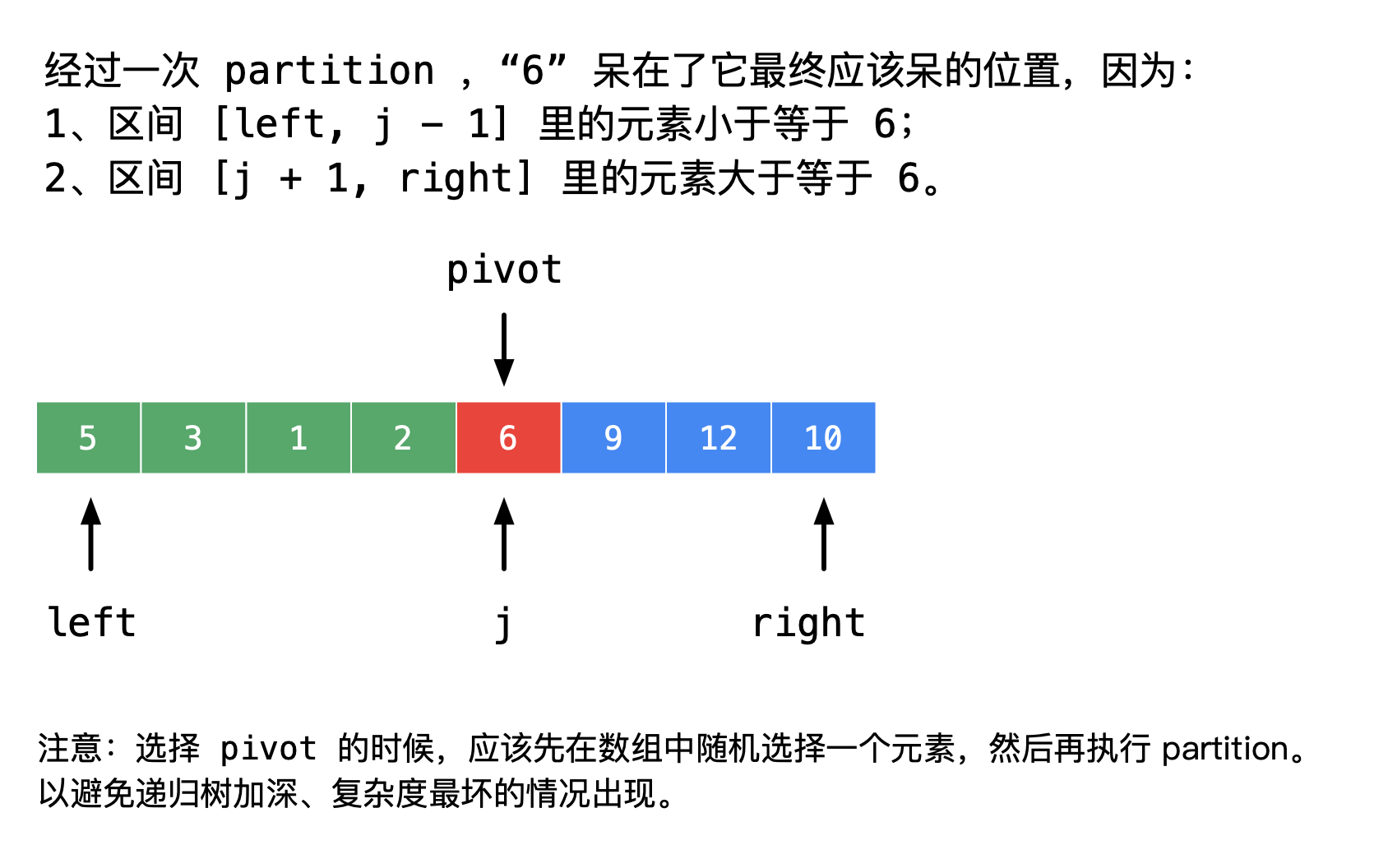
image.png

代码

为了应对极端测试用例，使得递归树加深，可以在循环一开始的时候，随机交换第 1 个元素与它后面的任意 1 个元素的位置；

说明：最极端的是顺序数组与倒序数组，此时递归树画出来是链表，时间复杂度是 O(N^2)，根本达不到减治的效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
import java.util.Random;

public class Solution {

  private static Random random = new Random(System.currentTimeMillis());

  public int findKthLargest(int[] nums, int k) {
    int len = nums.length;
    // 转换一下，第 k 大元素的索引是 len - k
    int target = len - k;
    int left = 0;
    int right = len - 1;
    while (true) {
      int index = partition(nums, left, right);
      if (index < target) {
        left = index + 1;
      } else if (index > target) {
        right = index - 1;
      } else {
        return nums[index];
      }
    }
  }

  /**
       * 在数组 nums 的子区间 [left, right] 执行 partition 操作，返回 nums[left] 排序以后应该在的位置
       * 在遍历过程中保持循环不变量的语义
       * 1、[left + 1, i] < nums[left]
       * 2、(i, j] >= nums[left]
       *
       * @param nums
       * @param left
       * @param right
       * @return
       */
  private int partition(int[] nums, int left, int right) {
    // 在区间随机选择一个元素作为标定点
    if (right > left) {
      // int randomIndex = left + 1 + random.nextInt(right - left);
      // swap(nums, left, randomIndex);
      swap(nums, left, (int) (Math.random() * (right - left) + left));
    }

    int pivot = nums[left];
    int i = left;
    for (int j = left + 1; j <= right; j++) {
      if (nums[j] < pivot) {
        // 小于 pivot 的元素都被交换到前面
        i++;
        swap(nums, i, j);
      }
    }
    // 在之前遍历的过程中，满足 [left + 1, i] < pivot，并且 (i, j] >= pivot
    swap(nums, left, i);
    // 交换以后 [left, i - 1] < pivot, nums[i] = pivot, [i + 1, right] >= pivot
    return i;
  }

  private void swap(int[] nums, int i, int j) {
    if(i != j) {
      int temp = nums[i];
      nums[i] = nums[j];
      nums[j] = temp;
    }
  }
} 


var findKthLargest = function(nums, k) {
  let len = nums.length, 
      // 转换一下，第 k 大元素的索引是 len - k
      target = len - k, 
      left = 0,
      right = len - 1

  while(true) {
    let index = partition(nums, left, right)
    if(index === target) {
      return nums[index]
    } else if (index > target) {
      right = index - 1
    } else {
      left = index + 1
    }
  }
};

/**
    * 在数组 nums 的子区间 [left, right] 执行 partition 操作，返回 nums[left] 排序以后应该在的位置
    * 在遍历过程中保持循环不变量的语义
    * 1、[left + 1, i] < nums[left]
    * 2、(i, j] >= nums[left]
    *
    * @param nums
    * @param left
    * @param right
    * @return
    */
var partition = function(nums, left, right) {
  // 在区间随机选择一个元素作为标定点
  if(right > left) {
    let temp = Math.floor(Math.random() * (right - left + 1)) + left
    swap(nums, temp, right)
  }
  let pivot = nums[left], i = left
  for(let j = left + 1; j <= right; j++) {
    if(nums[j] < pivot) {
      // 小于 pivot 的元素都被交换到前面
      i++
      swap(nums, i, j)
    }
  }
  // 在之前遍历的过程中，满足 [left + 1, i] < pivot，并且 (i, j] >= pivot
  swap(nums, left, i)
  // 交换以后 [left, i - 1] < pivot, nums[i] = pivot, [i + 1, right] >= pivot
  return i
}

var swap = function(nums, left, right) {
  if(left !== right) {
    let temp = nums[left]
    nums[left] = nums[right]
    nums[right] = temp
  }
}

复杂度分析：

  • 时间复杂度：O(N)，这里 N 是数组的长度。用主定理分析：

    复杂度：T(n) = T(n/2) + n

    首先不是一个完全的递归树，按照每次排序刚好定位到中间来想，递归树的下一层只有T(n/2)，不考虑另一半；

    其次，每一层递归树都要遍历对应的, “分而治之”的”分“后的数组长度，所以+n 这样来算

    用Master method，T(n) = aT(n/b) + f(n), f(n) = n,a=1,b=2, f(n) = Ω(n的 (以b为底a的对数 + x) 次方 )，x>0, 所以T(n) = O(f(n))=O(n)

    第一次交换，算法复杂度为O(N)。这里在确定基准值的相对位置（在K的左边或者右边）之后不用再对剩下的一半进行处理。也就是说第二次插入的算法复杂度不再是O(N)而是O(N/2)，接下来的过程是1+1/2+1/4+…….. < 2，换句话说就是一共是O(2N)的算法复杂度也就是O(N)的算法复杂度。

  • 空间复杂度：O(1)，原地排序，没有借助额外的辅助空间。

执行结果：通过

  • 执行用时：1 ms, 在所有 Java 提交中击败了99.09%的用户

  • 内存消耗：38.3 MB, 在所有 Java 提交中击败了97.33%的用户

方法三：基于堆排序的选择方法

排序思想

建立一个大根堆，做 k - 1次删除操作后堆顶元素就是我们要找的答案。堆排序过程中，不全部下沉，下沉nums.length-k+1,然后堆顶可以拿到我们top k答案了

  • 将待排序序列构造成一个大顶堆

    • 注意：这里使用的是数组，而不是一颗二叉树

  • 此时：整个序列的 最大值就是堆顶的根节点

  • 将其 与末尾元素进行交换，此时末尾就是最大值

  • 然后将剩余 n-1 个元素重新构造成一个堆，这样 就会得到 n 个元素的次小值。如此反复，便能的得到一个有序序列。

堆排序步骤图解

对数组 4,6,8,5,9 进行堆排序，将数组升序排序。

步骤一：构造初始堆

  1. 给定无序序列结构 如下：注意这里的操作用数组，树结构只是参考理解
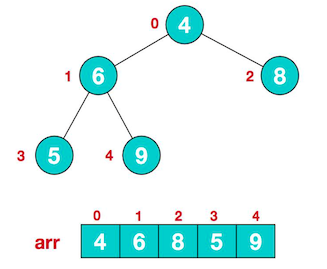
image.png

将给定无序序列构造成一个大顶堆。

  1. 此时从最后一个非叶子节点开始调整，从左到右，从上到下进行调整。
    叶节点不用调整，第一个非叶子节点 arr.length/2-1 = 5/2-1 = 1 ，也就是 元素为 6 的节点。

比较时：先让 5 与 9 比较，得到最大的那个，再和 6 比较，发现 9 大于 6，则调整他们的位置。

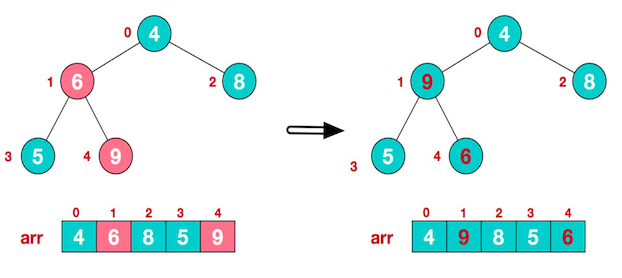
image.png
  1. 找到第二个非叶子节点 4，由于 [4,9,8] 中，9 元素最大，则 4 和 9 进行交换
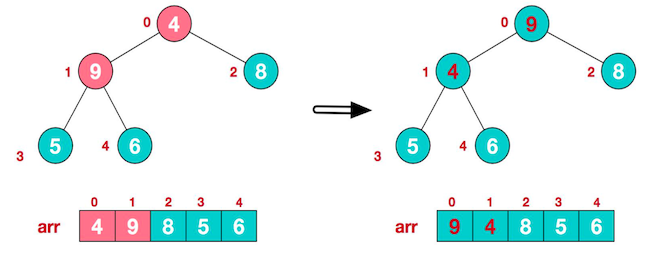
image.png
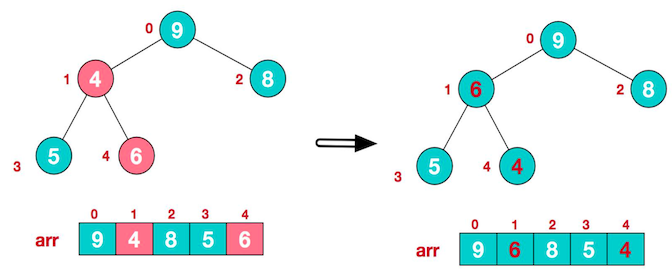
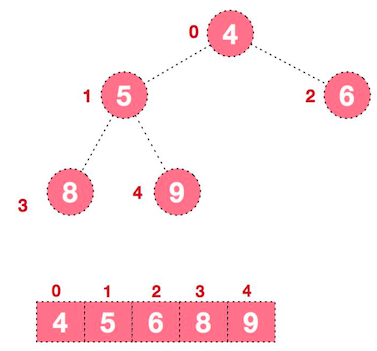
  1. 此时，交换导致了子根 [4,5,6] 结构混乱，将其继续调整。[4,5,6] 中 6 最大，将 4 与 6 进行调整。image.png

此时，就将一个无序序列构造成了一个大顶堆。

步骤二：将堆顶元素与末尾元素进行交换

将堆顶元素与末尾元素进行交换，使其末尾元素最大。然后继续调整，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

  1. 将堆顶元素 9 和末尾元素 4 进行交换

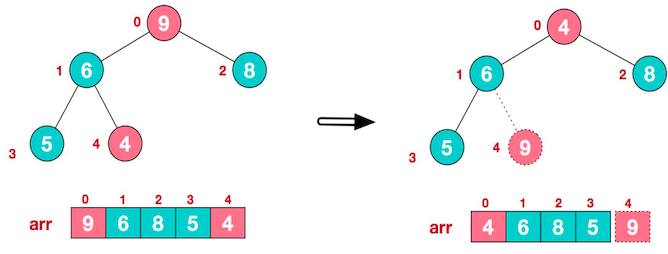
    image.png

  2. 重新调整结构，使其继续满足堆定义

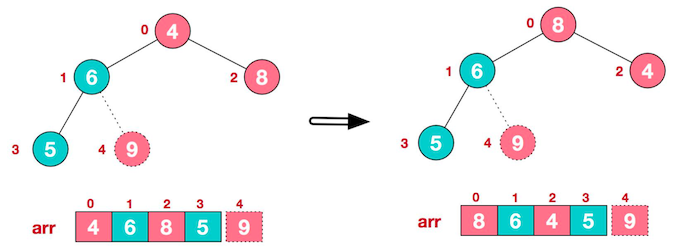
    image.png

  3. 再将堆顶元素 8 与末尾元素 5 进行交换，得到第二大元素 8

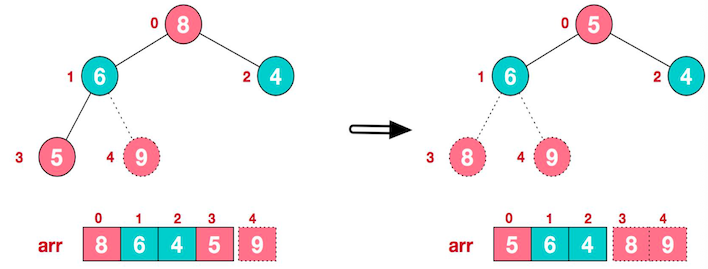
image.png

  1. 后续过程，继续进行调整、交换，如此反复进行，最终使得整个序列有序

    image.png

总结思路

  1. 将无序序列构建成一个堆，根据升序降序需求选择大顶堆
  2. 将堆顶元素与末尾元素交换，将最大元素「沉」到数组末端
  3. 重新调整结构，使其满足堆定义，然后继续交换堆顶与当前末尾元素，反复执行调整、交换步骤，直到整个序列有序。

注意事项

  1. 第一步构建初始堆
    • 是自底向上构建，从最后一个非叶子节点开始。
  2. 第二步下沉操作
    • 让尾部元素与堆顶元素交换，最大值被放在数组末尾，并且缩小数组的length，不参与后面大顶堆的调整
  3. 第三步调整
    • 是从上到下，从左到右,因为堆顶元素下沉到末尾了，要重新调整这颗大顶堆

代码

可以参考作为堆排序的模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
class Solution {
  // 整个流程就是上浮下沉
  public int findKthLargest(int[] nums, int k) {
    int heapSize = nums.length;
    buildMapHeap(nums, heapSize); // 构建好了一个大顶堆
    // 进行下沉 大顶堆是最大元素下沉到末尾
    for(int i = nums.length - 1; i >= nums.length - k + 1; i--) {
      swap(nums, 0, i);
      --heapSize; // 下沉后的元素不参与到大顶堆的调整
      maxHeapify(nums, 0, heapSize); // 重新调整大顶堆
    }
    return nums[0];
  }

  // 自下而上构建一颗大顶堆
  public void buildMapHeap(int[] nums, int heapSize) {
    for(int i = (int)(Math.floor(heapSize / 2) - 1); i >= 0; i--) {
      maxHeapify(nums, i, heapSize);
    }
  }

  // 从左向右，自上而下的调整节点
  public void maxHeapify(int[] nums, int i, int heapSize) {
    int l = i * 2 + 1, r = i * 2 + 2, largest = i;
    if(l < heapSize && nums[l] > nums[largest]) {
      largest = l;
    }
    if(r < heapSize && nums[r] > nums[largest]) {
      largest = r;
    }
    if(largest != i) {
      swap(nums, i, largest); // 进行节点调整
      // 继续调整下面的非叶子节点
      maxHeapify(nums, largest, heapSize);
    }
  }

  public void swap(int[] nums, int i, int j) {
    int temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
  }
}

// 整个流程就是上浮下沉
var findKthLargest = function(nums, k) {
    let heapSize = nums.length
    buildMaxHeap(nums, heapSize) // 构建好了一个大顶堆
    // 进行下沉 大顶堆是最大元素下沉到末尾
    for(let i = nums.length - 1; i >= nums.length - k + 1; i--) {
        swap(nums, 0, i)
        --heapSize // 下沉后的元素不参与到大顶堆的调整
        maxHeapify(nums, 0, heapSize) // 重新调整大顶堆
    }
    return nums[0]
};

// 自下而上构建一颗大顶堆
var buildMaxHeap = function(nums, heapSize) {
    for(let i = Math.floor(heapSize / 2) - 1; i >= 0; i--) {
        maxHeapify(nums, i, heapSize)
    }
}

// 从左向右，自上而下的调整节点
var maxHeapify = function(nums, i, heapSize) {
    let left = i * 2 + 1, right = i * 2 + 2, largest = i
    if(left < heapSize && nums[left] > nums[largest]) {
        largest = left
    }
    if(right < heapSize && nums[right] > nums[largest]) {
        largest = right
    }
    if(largest !== i) {
        swap(nums, i, largest) // 进行节点调整
        // 继续调整下面的非叶子节点
        maxHeapify(nums, largest, heapSize)
    }
}

var swap = function(nums, left, right) {
    let temp = nums[left]
    nums[left] = nums[right]
    nums[right] = temp
}

进行堆排序

1
2
findKthLargest(nums,nums.length)
// 或者调整一下 let i=nums.length-1;i>=nums.length-k+1;的条件就行

复杂度分析

  • 时间复杂度：O(nlogn)，建堆的时间代价是 O(n)，删除的总代价是 O(klogn)，因为 k<n，故渐进时间复杂为 O(n+klogn)=O(nlogn)。
  • 空间复杂度：O(1)。只需要常数的空间存放若干变量。

执行结果：通过

  • 执行用时：2 ms, 在所有 Java 提交中击败了89.59%的用户

  • 内存消耗：38.6 MB, 在所有 Java 提交中击败了76.42%的用户