有效的数独

请你判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
数独部分空格内已填入了数字，空白格用 ‘.’ 表示。

注意：

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。

示例 1：

输入：board =
[[“5”,”3”,”.”,”.”,”7”,”.”,”.”,”.”,”.”]
,[“6”,”.”,”.”,”1”,”9”,”5”,”.”,”.”,”.”]
,[“.”,”9”,”8”,”.”,”.”,”.”,”.”,”6”,”.”]
,[“8”,”.”,”.”,”.”,”6”,”.”,”.”,”.”,”3”]
,[“4”,”.”,”.”,”8”,”.”,”3”,”.”,”.”,”1”]
,[“7”,”.”,”.”,”.”,”2”,”.”,”.”,”.”,”6”]
,[“.”,”6”,”.”,”.”,”.”,”.”,”2”,”8”,”.”]
,[“.”,”.”,”.”,”4”,”1”,”9”,”.”,”.”,”5”]
,[“.”,”.”,”.”,”.”,”8”,”.”,”.”,”7”,”9”]]
输出：true

示例 2：
输入：board =
[[“8”,”3”,”.”,”.”,”7”,”.”,”.”,”.”,”.”]
,[“6”,”.”,”.”,”1”,”9”,”5”,”.”,”.”,”.”]
,[“.”,”9”,”8”,”.”,”.”,”.”,”.”,”6”,”.”]
,[“8”,”.”,”.”,”.”,”6”,”.”,”.”,”.”,”3”]
,[“4”,”.”,”.”,”8”,”.”,”3”,”.”,”.”,”1”]
,[“7”,”.”,”.”,”.”,”2”,”.”,”.”,”.”,”6”]
,[“.”,”6”,”.”,”.”,”.”,”.”,”2”,”8”,”.”]
,[“.”,”.”,”.”,”4”,”1”,”9”,”.”,”.”,”5”]
,[“.”,”.”,”.”,”.”,”8”,”.”,”.”,”7”,”9”]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与示例1 相同。但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

方法一：数组解法

由于只要我们判断是否为有效的数独。

所以我们只需要对 board 中出现的数进行判断，如果 board 中有数违反了数独的规则，返回 false，否则返回 true。

我们可以使用数组来记录某行/某列/某个小方块出现过哪些数字，来帮助我们判断是否符合「有效数独」的定义。

这道题唯一的难点可能是在于如何确定某个数落在哪个小方块中，我们可以去小方块进行编号：

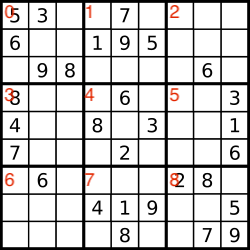
然后推导出小方块编号和行列的关系为： idx = i / 3 * 3 + j / 3。

class Solution {
    public boolean isValidSudoku(char[][] board) {
       boolean[][] row = new boolean[9][9], col = new boolean[9][9], area = new boolean[9][9];
       for(int i = 0; i < 9; i++) {
           for(int j = 0; j < 9; j++) {
               if(board[i][j] == '.') continue;
               int c = board[i][j] - '1';
                 int idx = i / 3 * 3 + j / 3;
               if(!row[i][c] && !col[j][c] && !area[idx][c]) {
                   row[i][c] = col[j][c] = area[idx][c] = true;
               } else {
                   return false;
               }
           }
       }
       return true;
    }
}

复杂度分析

时间复杂度：O(1)，在固定 9*9 的问题里，复杂度不随数据变化而变化。
空间复杂度：O(1)，在固定 9*9 的问题里，复杂度不随数据变化而变化。

执行结果：通过

执行用时：2 ms, 在所有 Java 提交中击败了91.20%的用户
内存消耗：38.6 MB, 在所有 Java 提交中击败了39.79%的用户