题目描述:给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]示例 2:
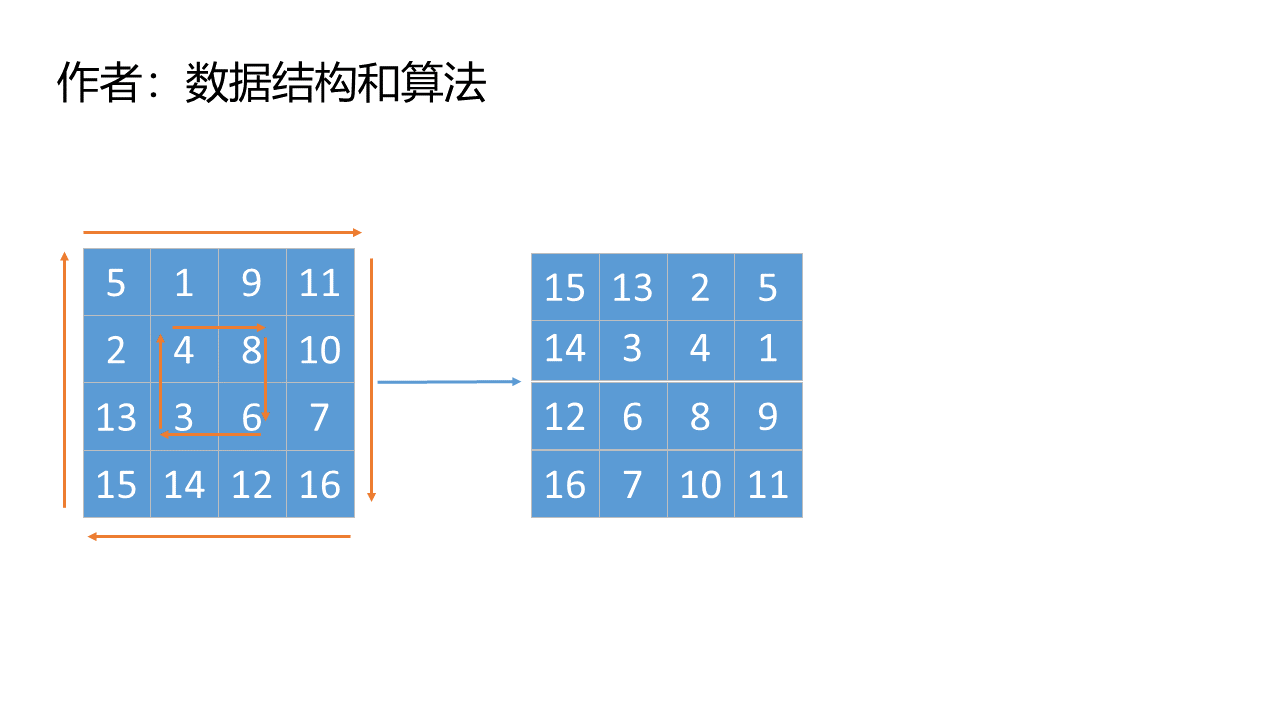
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]示例 3:
输入:matrix = [[1]]
输出:[[1]]示例 4:
输入:matrix = [[1,2],[3,4]]
输出:[[3,1],[4,2]]
方法一:两次翻转

1 | class Solution { |
复杂度分析
时间复杂度:O(N^2),其中 N 是 matrix 的边长。对于每一次翻转操作,我们都需要枚举矩阵中一半的元素。
空间复杂度:O(1)。为原地翻转得到的原地旋转。
执行结果:通过
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:38.4 MB, 在所有 Java 提交中击败了74.28%的用户
方法二:原地旋转
题中说了是顺时针旋转90度,通过旋转其实可以发现一个规律,只需要一圈一圈的旋转即可
1 | class Solution { |
复杂度分析
时间复杂度:O(N^2),其中 N 是 matrix 的边长
空间复杂度:O(1)。为原地旋转。
执行结果:通过
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:38.6 MB, 在所有 Java 提交中击败了50.85%的用户