题目描述:给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
方法一:快排
不稳定排序
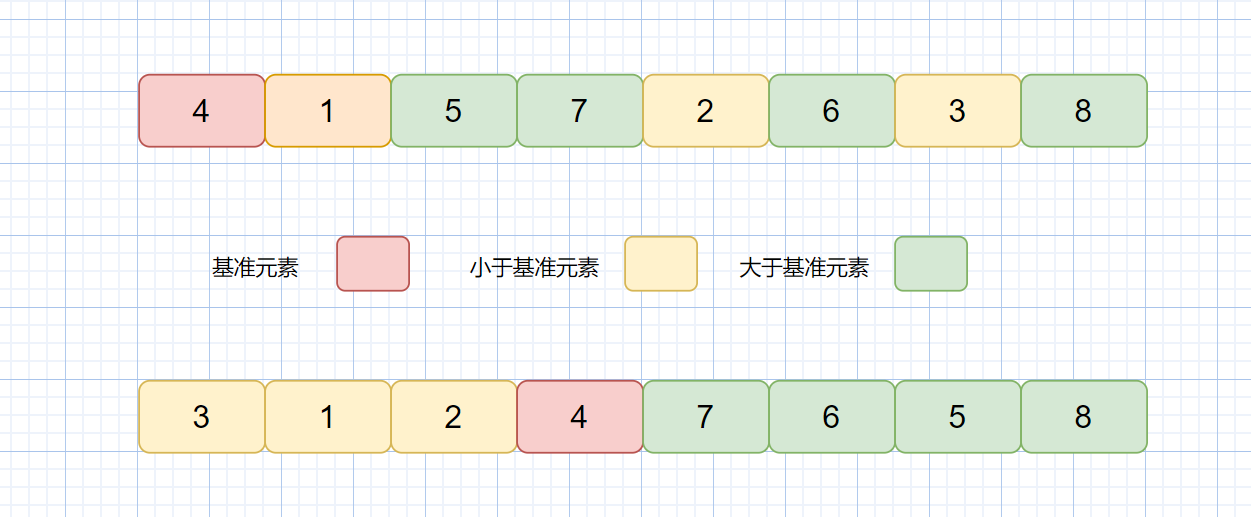
先从数组中找一个基准数
让其他比它大的元素移动到数列一边,比他小的元素移动到数列另一边,从而把数组拆解成两个部分。
再对左右区间重复第二步,直到各区间只有一个数。
1 | import java.util.Random; |
1 | var sortArray = function(nums) { |
复杂度分析:
时间复杂度:O(nlogn),这里 N 是数组的长度。第一次交换,算法复杂度为O(N),然后继续处理两边的数据,再合并,合并操作的算法复杂度是O(1),于是总的算法复杂度是O(N*logN)(可以这么理解,每次交换用了N,一共logN次)
空间复杂度:O(h),其中 h 为递归调用的层数。最坏情况下需 O(n) 的空间,最优情况下每次都平衡,此时整个递归树高度为 logn,空间复杂度为 O(logn)。
执行结果:通过
执行用时:11 ms, 在所有 Java 提交中击败了85.37%的用户
内存消耗:47.4 MB, 在所有 Java 提交中击败了63.49%的用户
方法二:堆排序
不稳定排序
将待排序序列构造成一个大顶堆
- 注意:这里使用的是数组,而不是一颗二叉树
此时:整个序列的 最大值就是堆顶的根节点
将其 与末尾元素进行交换,此时末尾就是最大值
然后将剩余 n-1 个元素重新构造成一个堆,这样 就会得到 n 个元素的次小值。如此反复,便能的得到一个有序序列。
1 | class Solution { |
1 | var sortArray = function(nums) { |
复杂度分析
时间复杂度:O(nlogn)。初始化建堆的时间复杂度为 O(n),建完堆以后需要进行 n−1 次调整,一次调整(即 maxHeapify) 的时间复杂度为 O(logn),那么 n−1 次调整即需要 O(nlogn) 的时间复杂度。因此,总时间复杂度为 O(n+nlogn)=O(nlogn)。
空间复杂度:O(1)。只需要常数的空间存放若干变量。
执行结果:通过
执行用时:11 ms, 在所有 Java 提交中击败了85.37%的用户
内存消耗:47.4 MB, 在所有 Java 提交中击败了63.49%的用户