寻找重复数

题目描述：给定一个包含 n + 1 个整数的数组 nums ，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有一个重复的整数，找出这个重复的数。

你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。

示例 1：
输入：nums = [1,3,4,2,2]
输出：2

示例 2：
输入：nums = [3,1,3,4,2]
输出：3

示例 3：
输入：nums = [1,1]
输出：1

示例 4：
输入：nums = [1,1,2]
输出：1

理解题意：

n + 1 个整数，放在长度为 n 的数组里，根据「抽屉原理」，至少会有 1 个整数是重复的；

抽屉原理：把 10 个苹果放进 9 个抽屉，一定存在某个抽屉放至少 2 个苹果。

二分查找

思路：

先猜一个数（有效范围 [left..right] 里位于中间的数 mid），然后统计原始数组中小于等于 mid 的元素的个数 cnt：
- 如果 cnt 严格大于 mid。根据抽屉原理，重复元素就在区间 [left..mid] 里；
- 否则，重复元素就在区间 [mid + 1..right] 里。

与绝大多数使用二分查找问题不同的是，这道题正着思考是容易的，即：思考哪边区间存在重复数是容易的，因为有抽屉原理做保证。

public class Solution {

  public int findDuplicate(int[] nums) {
    int len = nums.length;
    int left = 1;
    int right = len - 1;
    while (left < right) {
      int mid = left + (right - left) / 2;

      int cnt = 0;
      for (int num : nums) {
        if (num <= mid) {
          cnt += 1;
        }
      }

      // 根据抽屉原理，小于等于 4 的个数如果严格大于 4 个，此时重复元素一定出现在 [1..4] 区间里
      if (cnt > mid) {
        // 重复元素位于区间 [left..mid]
        right = mid;
      } else {
        // if 分析正确了以后，else 搜索的区间就是 if 的反面区间 [mid + 1..right]
        left = mid + 1;
      }
    }
    return left;
  }
}

var findDuplicate = function(nums) {
  let left = 1, right = nums.length - 1
  while(left < right) {
    let mid = Math.floor((right - left) / 2 + left)
    let cnt = 0
    for(let num of nums) {
      if(num <= mid) {
        cnt++
      }
    }
    // 根据抽屉原理，小于等于 4 的个数如果严格大于 4 个，此时重复元素一定出现在 [1..4] 区间里
    if(cnt > mid) {
      right = mid
    } else {
      // if 分析正确了以后，else 搜索的区间就是 if 的反面区间 [mid + 1..right]
      left = mid + 1
    }
  }
  return left
};

解释：

题目中说：长度为 n + 1 的数组，数值在 1 到 n 之间。因此长度为 len，数值在 1 到 len - 1 之间；
使用 while (left < right) 与 right = mid; 和 left = mid + 1; 配对的写法是为了保证退出循环以后 left 与 right 重合，left （或者 right）就是我们要找的重复的整数；
在循环体内，先猜一个数 mid，然后遍历「输入数组」，统计小于等于 mid 的元素个数 cnt，如果 cnt > mid 说明重复元素一定出现在 [left..mid] 因此设置 right = mid；

复杂度分析：

时间复杂度：O(NlogN)，二分法的时间复杂度为 O(logN)，在二分法的内部，执行了一次 for 循环，时间复杂度为 O(N)，故时间复杂度为 O(NlogN)
空间复杂度：O(1)，使用了一个 cnt 变量，因此空间复杂度为 O(1)

执行结果：通过

执行用时：27 ms, 在所有 Java 提交中击败了30.86%的用户
内存消耗：53.8 MB, 在所有 Java 提交中击败了83.73%的用户

以数组 [1,3,4,2,2] 为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)，
其映射关系 n->f(n) 为：
0->1
1->3
2->4
3->2
4->2
同样的，我们从下标为 0 出发，根据 f(n)f(n) 计算出一个值，以这个值为新的下标，再用这个函数计算，以此类推产生一个类似链表一样的序列。
0->1->3->2->4->2->4->2->……
这里 2->4 是一个循环，那么这个链表可以抽象为下图：

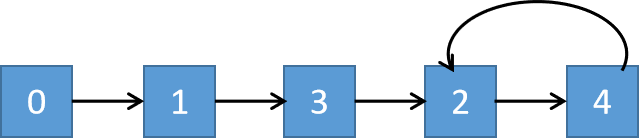
从理论上讲，数组中如果有重复的数，那么就会产生多对一的映射，这样，形成的链表就一定会有环路了，

综上

数组中有一个重复的整数 <==> 链表中存在环

找到数组中的重复整数 <==> 找到链表的环入口

慢指针走一步 slow = slow.next ==> 本题 slow = nums[slow]
快指针走两步 fast = fast.next.next ==> 本题 fast = nums[nums[fast]]

class Solution {
  public int findDuplicate(int[] nums) {
    int slow = 0, fast = 0;
    slow = nums[slow];
    fast = nums[nums[fast]];
    while(slow != fast) {
      slow = nums[slow];
      fast = nums[nums[fast]];
    }
    fast = 0;
    while (slow != fast) {
      slow = nums[slow];
      fast = nums[fast];
    }
    return slow;
  }
}

var findDuplicate = function(nums) {
  let slow = 0, fast = 0
  slow = nums[slow]
  fast = nums[nums[fast]]
  while(slow !== fast) {
    slow = nums[slow]
    fast = nums[nums[fast]]
  }
  fast = 0
  while(slow !== fast) {
    slow = nums[slow]
    fast = nums[fast]
  }
  return slow
};

复杂度分析

时间复杂度：O(n)
空间复杂度：O(1)。我们只需要常数空间存放若干变量。

执行结果：通过

执行用时：4 ms, 在所有 Java 提交中击败了94.95%的用户
内存消耗：53.9 MB, 在所有 Java 提交中击败了81.44%的用户

二分查找

思路：

快慢指针