实现strStr()

发表于 | 分类于 |
字数统计: 1.6k 字 | 阅读时长 ≈ 6 分钟

题目描述：实现 strStr() 函数。

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回  -1 。

 

说明：

  • 当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。
  • 对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。

示例 1：
输入：haystack = “hello”, needle = “ll”
输出：2

示例 2：
输入：haystack = “aaaaa”, needle = “bba”
输出：-1

示例 3：
输入：haystack = “”, needle = “”
输出：0

方法一：KMP算法

什么是 KMP

因为是由这三位学者发明的：Knuth，Morris和Pratt，取了三位学者名字的首字母。

KMP 有什么用

主要应用在字符串匹配上。主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。

KMP 重点

如何记录已经匹配的文本内容=>使用 next 数组（前缀表）

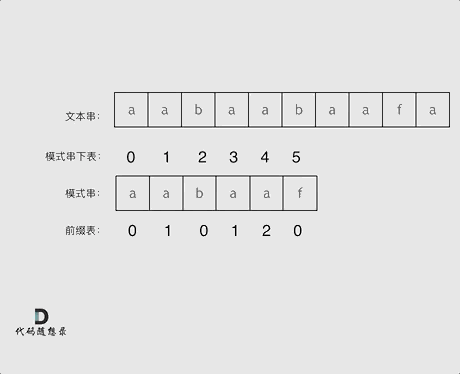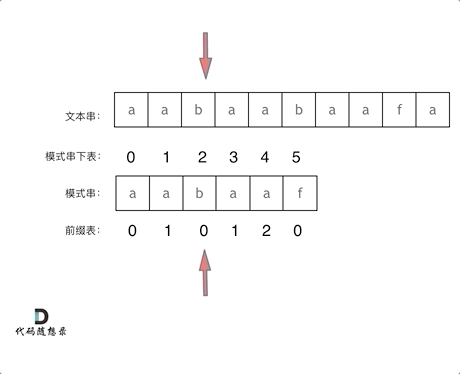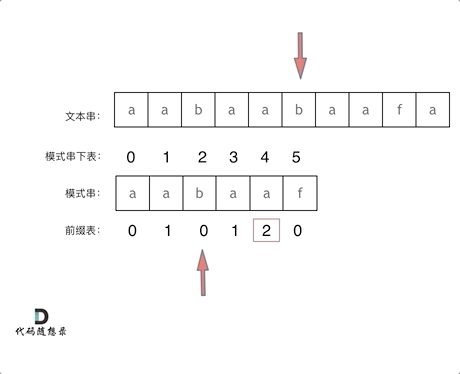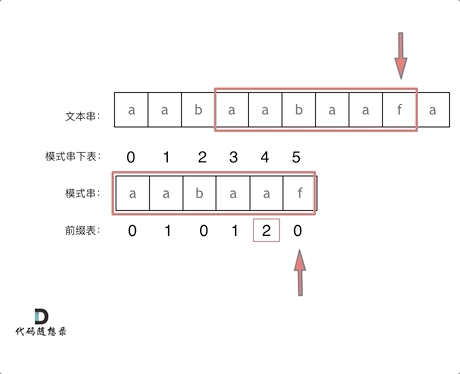
什么是前缀表

next数组就是一个前缀表（prefix table）。

是什么：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

作用：用来回退，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

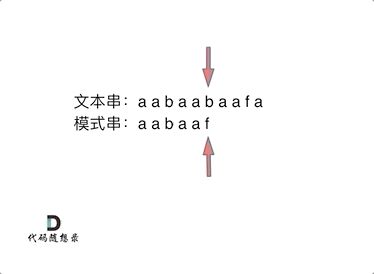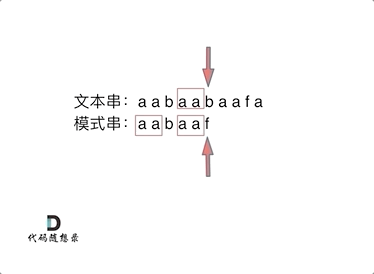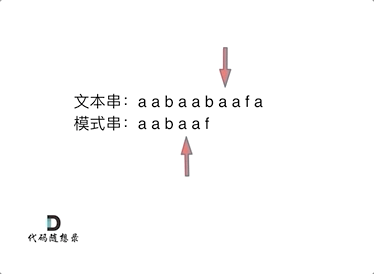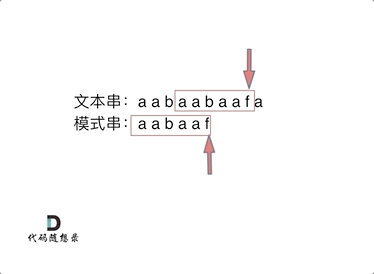
KMP精讲1.gif

如何计算前缀表

长度为前1个字符的子串a，最长相同前后缀的长度为0。（注意字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。）

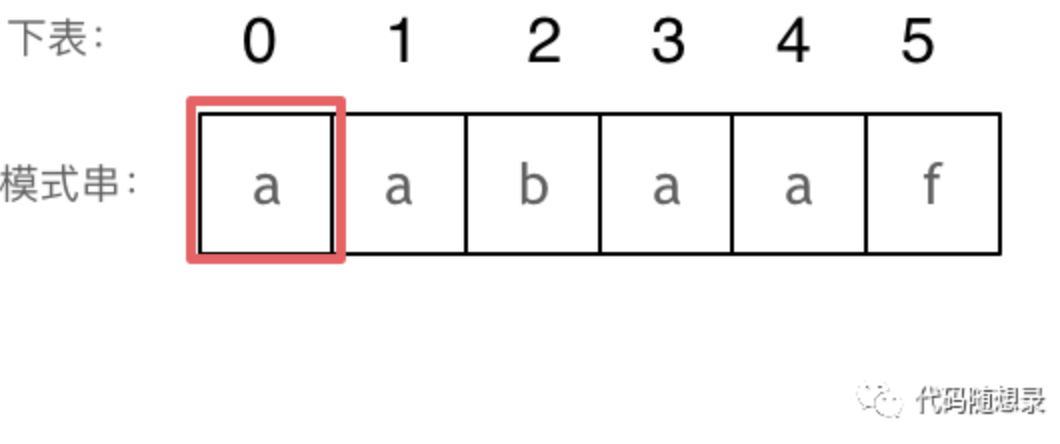
KMP精讲5.png

长度为前2个字符的子串aa，最长相同前后缀的长度为1。

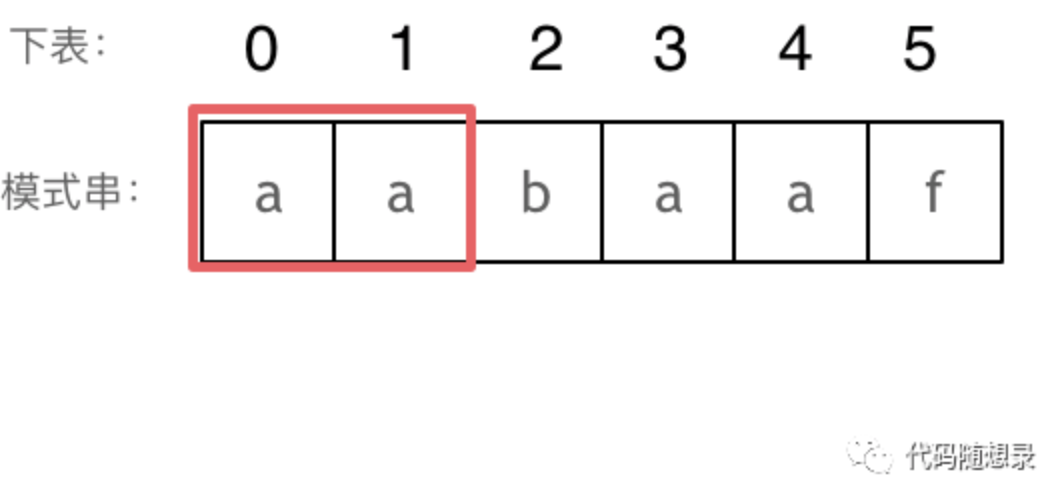
KMP精讲6.png

长度为前3个字符的子串aab，最长相同前后缀的长度为0。

KMP精讲7.png

以此类推：

  • 长度为前4个字符的子串aaba，最长相同前后缀的长度为1。

  • 长度为前5个字符的子串aabaa，最长相同前后缀的长度为2。

  • 长度为前6个字符的子串aabaaf，最长相同前后缀的长度为0。

那么把求得的最长相同前后缀的长度就是对应前缀表的元素

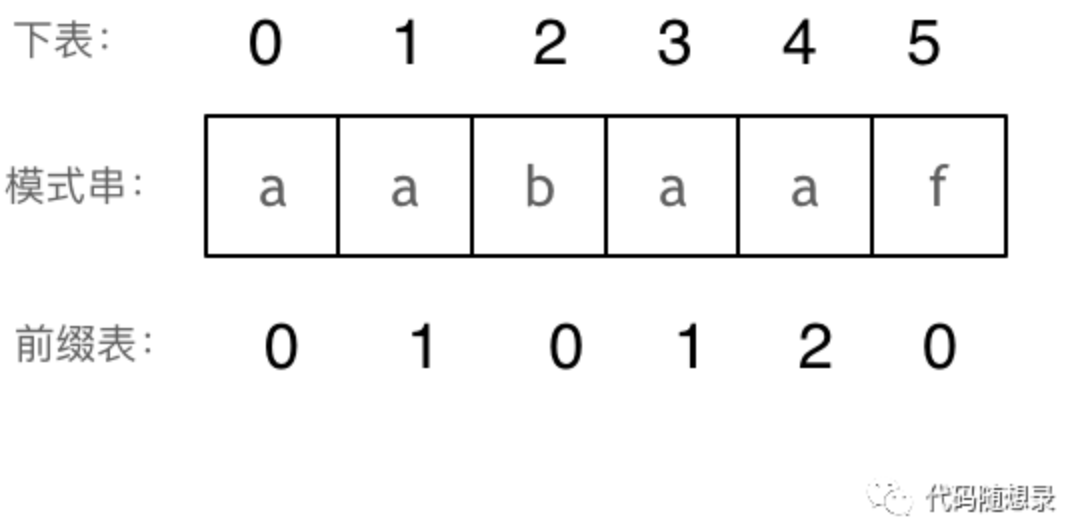
KMP精讲8.png

可以看出模式串与前缀表对应位置的数字表示的就是：下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

如何利用前缀表

如何利用前缀表当字符不匹配的时候应该指针应该移动的位置

  • 找到不匹配的位置时，我们要看它前一个字符的前缀表的数值是多少
    • 为什么要前一个字符的前缀表的数值呢？
      • 因为要找前面字符串的最长相同的前缀和后缀。
  • 然后把下标移动到前一个字符的前缀表数值处继续匹配

KMP精讲2.gif

时间复杂度分析

其中n为文本串长度，m为模式串长度。

因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。

所以整个KMP算法的时间复杂度是O(n+m)的。

如何构建 next 数组

构造next数组其实就是计算模式串s，前缀表的过程。 主要有如下三步：

  1. 初始化
  2. 处理前后缀不相同的情况
  3. 处理前后缀相同的情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function getNext(next, needle) {
  // 1. 初始化
  let i = 0; // 指向前缀终止位置
  next[0] = 0; // 0之前最长相等的前后缀长度
  // j 指向后缀终止位置
  for(let j = 1; j < needle.length; j ++) {
    // 2. 处理前后缀不相同的情况
    while(i > 0 && needle[i] !== needle[j]) {
      // 向前回溯
      // next数组记录了包括i与i之前的子串的相同前后缀的长度
      i = next[i - 1];
    }
    // 3. 处理前后缀相同的情况
    if(needle[i] === needle[j]) {
      i++;
    }
    // 需要将 i 前缀的长度赋值给 next[j]，因为next[j]要记录相同前后缀的长度
    next[j] = i;
  }
}

使用 next 数组来做匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 文本串 s、模式串 t
// 初始化：i 指向文本串，j 指向模式串
for(let i = 0, j = 0; i < s.length; i++) {
  // 如果不匹配
  while(j > 0 && s[i] !== t[j]) {
    j = next[j - 1]; // j 寻找之前匹配的位置
  }
  // 匹配，则指针向后移动
  if(s[i] === t[j]) {
    j++;
  }
  // 文本串出现了模式串
  if(j == t.length) {
    return i - t.length + 1;
  }
}

最终的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
var strStr = function(haystack, needle) {
  let n = haystack.length, m = needle.length;
  if (m == 0) {
    return 0;
  }

  let next =  getNext(needle);
  for(let i = 0, j = 0; i < haystack.length; i++) {
    // 如果不匹配
    while(j > 0 && haystack[i] !== needle[j]) {
      j = next[j - 1]; // j 寻找之前匹配的位置
    }
    // 匹配，则指针向后移动
    if(haystack[i] === needle[j]) {
      j++;
    }
    // 文本串出现了模式串
    if(j == m) {
      return i - m + 1;
    }
  }
  return -1;
};

var getNext = function(needle) {
  let next = new Array(needle.length)
  // 1. 初始化
  let i = 0; // 指向前缀终止位置
  next[0] = 0; // 0之前最长相等的前后缀长度
  // j 指向后缀终止位置
  for(let j = 1; j < needle.length; j ++) {
    // 2. 处理前后缀不相同的情况
    while(i > 0 && needle[i] !== needle[j]) {
      // 向前回溯
      // next数组记录了包括i与i之前的子串的相同前后缀的长度
      i = next[i - 1];
    }
    // 3. 处理前后缀相同的情况
    if(needle[i] === needle[j]) {
      i++;
    }
    // 需要将 i 前缀的长度赋值给 next[j]，因为next[j]要记录相同前后缀的长度
    next[j] = i;
  }
  return next
}

复杂度分析

  • 时间复杂度：O(n+m)
  • 空间复杂度：O(m)，其中 m 是字符串 needle 的长度。我们只需要保存字符串 needle 的前缀函数

执行结果：通过

  • 执行用时：88 ms, 在所有 JavaScript 提交中击败了46.87%的用户

  • 内存消耗：39.1 MB, 在所有 JavaScript 提交中击败了56.61%的用户