最长回文子串

发表于 | 分类于 |
字数统计: 885 字 | 阅读时长 ≈ 3 分钟

题目描述：给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = “babad”
输出：”bab”
解释：”aba” 同样是符合题意的答案。

示例 2：
输入：s = “cbbd”
输出：”bb”

示例 3：
输入：s = “a”
输出：”a”

示例 4：
输入：s = “ac”
输出：”a”

中心扩散法

两种情况

  • 一种是回文子串长度为奇数（如aba，中心是b）
  • 另一种回文子串长度为偶数（如abba，中心是b，b）

循环遍历字符串 对取到的每个值 都假设他可能成为最后的中心进行判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function longestPalindrome(s) {
  if (s.length < 2) {
    return s
  }
  let res = s[0];
  for (let i = 0; i < s.length; i++) {
    // 寻找长度为奇数的回文子串(以当前元素向两边扩散)
    const s1 = palindrome(s, i, i);
    // 寻找长度为偶数的回文子串(以s[i],s[i + 1])向两边扩散
    const s2 = palindrome(s, i, i + 1);
    res = res.length > s1.length ? res : s1;
    res = res.length > s2.length ? res : s2;
  }
  return res;
};

function palindrome(s, left, right) {
  // 左右指针，从s[left]和s[right]向两边扩散，找到最长回文串
  while (left >= 0 && right < s.length && s[left] == s[right]) {
    left--;
    right++;
  }
  // 注意此处 left,right 的值循环完后  是恰好不满足循环条件的时刻
  // 所以需要取 取[left + 1,right - 1]这个区间 
  return s.slice(left + 1, right);
}

复杂度

  • 时间复杂度：O(n^2)
  • 空间复杂度：O(1)

动态规划

定义状态

dp[i][j] 表示子串 s[i..j] 是否为回文子串，这里子串 s[i..j] 定义为左闭右闭区间，可以取到 s[i] 和 s[j] 。

初始化状态

整个 dp 二维数组为 false

情况分析

s[i]与s[j]相等，s[i]与s[j]不相等

  • 当s[i]与s[j]不相等，dp[i][j] 一定为 false
  • 当s[i]与s[j]相等时
    • 下标i 与 j相同，同一个字符例如a，当然是回文子串
    • 下标i 与 j相差为1，例如aa，也是文子串
    • 下标大于1时，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

遍历顺序

情况三是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的。

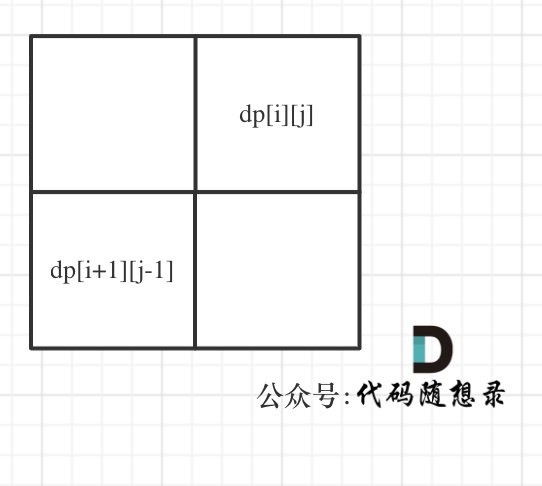
dp[i + 1][j - 1] 在 dp[i][j]的左下角，如图：

647.回文子串

如果这矩阵是从上到下，从左到右遍历，那么会用到没有计算过的dp[i + 1][j - 1]，也就是根据不确定是不是回文的区间[i+1,j-1]，来判断了[i,j]是不是回文，那结果一定是不对的。

所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const longestPalindrome = (s) => {
  if (s.length < 2) return s
  // res: 最长回文子串
  let res = s[0], dp = Array.from(Array(s.length), () => Array(s.length).fill(false));

  for (let i = s.length - 1; i >= 0; i--) {
    for (let j = i; j < s.length; j++) {
      if (s[i] == s[j]) { // 情况一
        if (j - i <= 1 || dp[i + 1][j - 1]) {  // 情况二、三
          dp[i][j] = true;
        }
      }


      // 获取当前最长回文子串
      if (dp[i][j] && j - i + 1 > res.length) {
        res = s.slice(i, j + 1)
      }
    }
  }
  return res
}

复杂度

  • 时间复杂度：O(n^2)
  • 空间复杂度：O(n^2)