全排列

题目描述：给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：
输入：nums = [1]
输出：[[1]]

全排列

• 每一位都有3种选择：1、2、3。

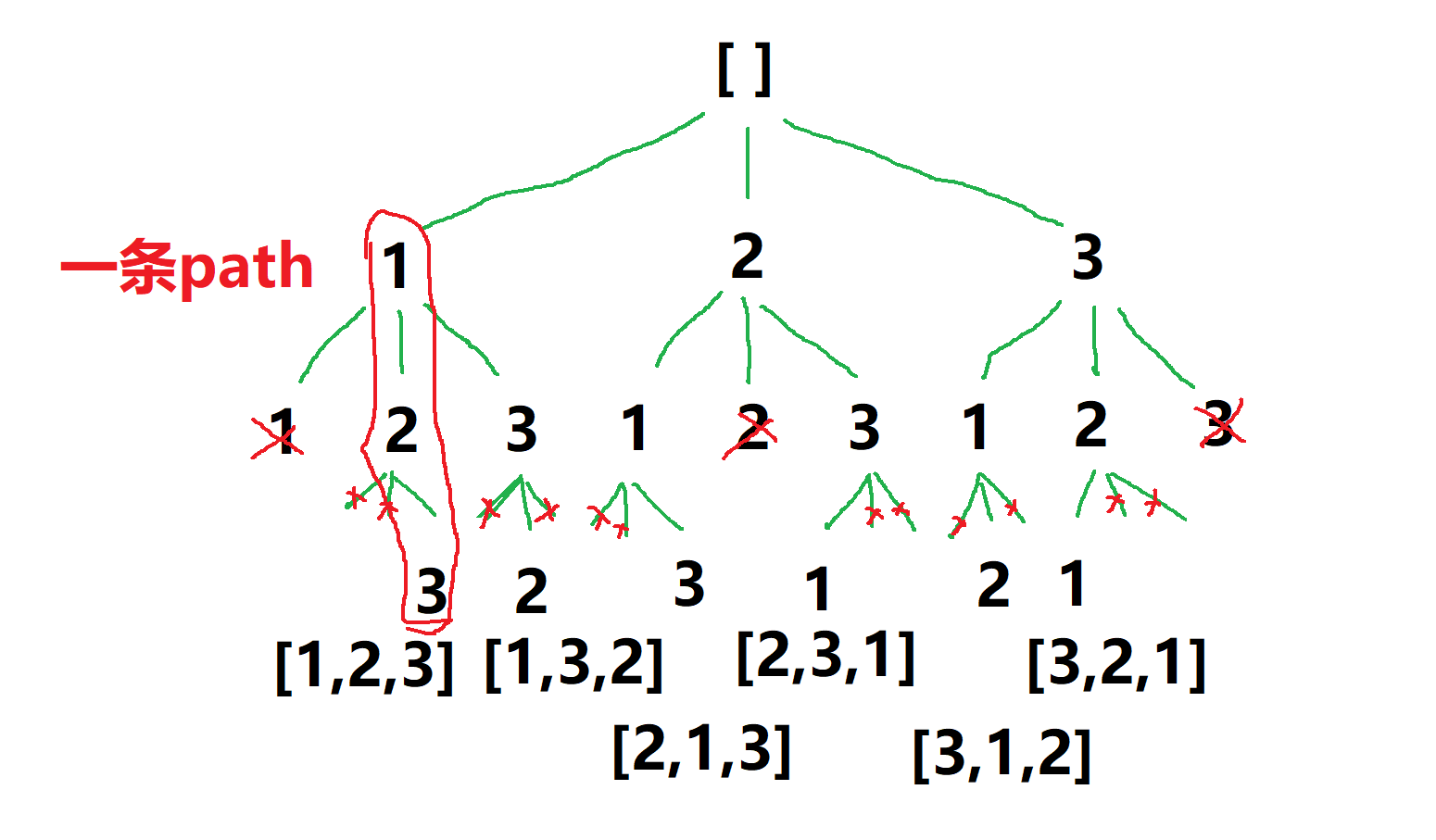
• 每一次都做选择，展开出一棵空间树，如下图。

• 利用约束条件「不能重复选」，做剪枝，剪去不会产生正确解的选项（分支）。

  • 利用 hashMap，记录选过的数，下次遇到相同的数，跳过。
  • 这样就不会进入「不会得出解的分支」，不做无效的搜索。

怎么写递归函数

• 我们要在这个包含解的空间树上，用 DFS 的方式搜索出所有的解。

• dfs 函数：基于当前的 path，继续选数，直到构建出合法的 path，加入解集。

  • 递归的入口：dfs 执行传入空 path，什么都还没选。

  • 函数体内，用 for loop 枚举出当前所有的选项，并用 if 语句跳过剪枝项。

    • 每一轮迭代，作出一个选择，基于它，继续选（递归调用）。

  • 递归的出口：当构建的 path 数组长度等于 nums 长度，就选够了，加入解集。

为什么要回溯

• 我们不是找到一个排列就完事，要找出所有满足条件的排列。

• 当一个递归调用结束，结束的是当前的递归分支，还要去别的分支继续搜。

• 所以，要撤销当前的选择，回到选择前的状态，再选下一个选项，即进入下一个分支。

• 注意，往 map 存入的当前选择也要撤销，表示撤销这个选择。

• 退回来，把路走全，才能在一棵空间树中，回溯出所有的解。

const permute = (nums) => {
  const res = [];
  const used = {};

  function dfs(path) {
    if (path.length == nums.length) { // 个数选够了
      res.push(path.slice()); // 拷贝一份path，加入解集res
      return;                 // 结束当前递归分支
    }
    for (const num of nums) { // for枚举出每个可选的选项
      // if (path.includes(num)) continue; // 别这么写！查找是O(n)，增加时间复杂度
      if (used[num]) continue; // 使用过的，跳过
      path.push(num);         // 选择当前的数，加入path
      used[num] = true;       // 记录一下 使用了
      dfs(path);              // 基于选了当前的数，递归
      path.pop();             // 上一句的递归结束，回溯，将最后选的数pop出来
      used[num] = false;      // 撤销这个记录
    }
  }

  dfs([]); // 递归的入口，空path传进去
  return res;
};

为什么加入解集时，要将数组内容拷贝到一个新的数组里，再加入解集？

因为该 path 变量存的是地址引用，结束当前递归时，将它加入 res 后，该算法还要进入别的递归分支继续搜索，还要继续将这个 path 传给别的递归调用，它所指向的内存空间还要继续被操作，所以 res 中的 path 的内容会被改变，这就不对。
所以要弄一份当前的拷贝，放入 res，这样后续对 path 的操作，就不会影响已经放入 res 的内容。

复杂度分析：

• 时间复杂度：O(n x n!)，其中 n 为序列的长度。

• 空间复杂度：O(n)。除答案数组以外，递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度